Review of Linear Algebra

Graphics’ Dependencies

Basic mathematics

Linear algebra
calculus
statistics

Basic Physics

Optics
Mechanics

Misc

Signal processing
Numerical analysis

A bit of Aesthetics

Vectors

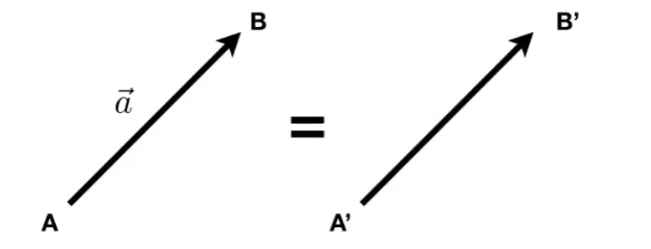
Usually written as \(\vec{a}\) or in bold \(\textbf{a}\)
or using start and end points \(\vec{AB} = B - A \)
Direction and length
No absolute starting position

Vector Normalization

Magnitude of a vector written as \( \vec{a} \)

Unit Vector

A vector with magnitude of 1

Finding the unit vector of a vector (normalization): \(\hat{a} = \vec{a} /

\vec{a}

Used to represent directions

Vector Addition

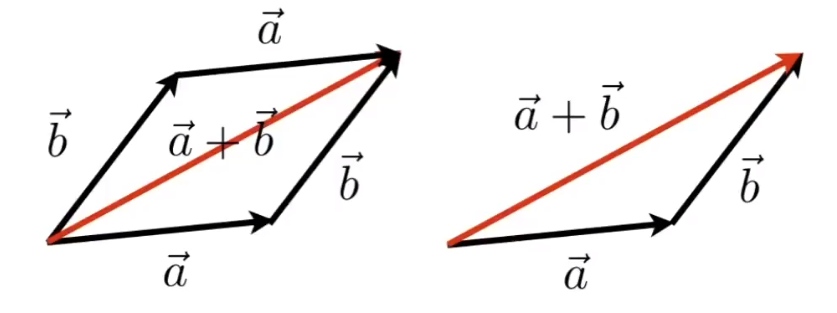
Geometrically: Parallelogram law & Triangle law
Algebraically: Simply and coordinates

Cartesian Coordinates

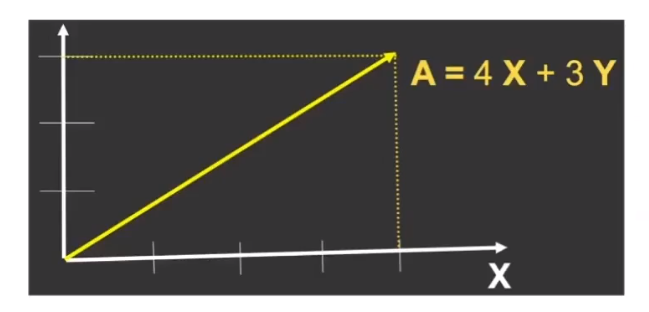
X and Y can be any (usually orthogonal unit) vectors

\[A\ =\ \begin{pmatrix} x\\ y \end{pmatrix}\ A^\top=(x, y)\ ||A|| = \sqrt{x^2 + y^2}\]

Vector Multiplication

Dot Product

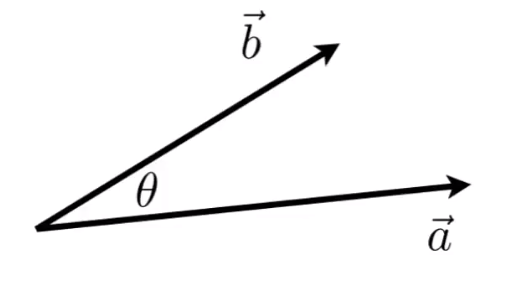
\[\vec{a} \cdot \vec{b} = ||\vec{a}|| ||\vec{b}|| cos\theta,\ cos\theta = \frac{\vec{a}\cdot\vec{b}}{||\vec{a}|| ||\vec{b}||}\]

for unit vectors: \(cos \theta = \vec{a} \cdot \vec{b}\)

Properties:

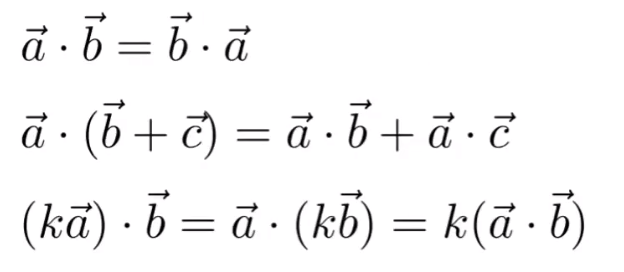
Component-wise multiplication, then adding up:

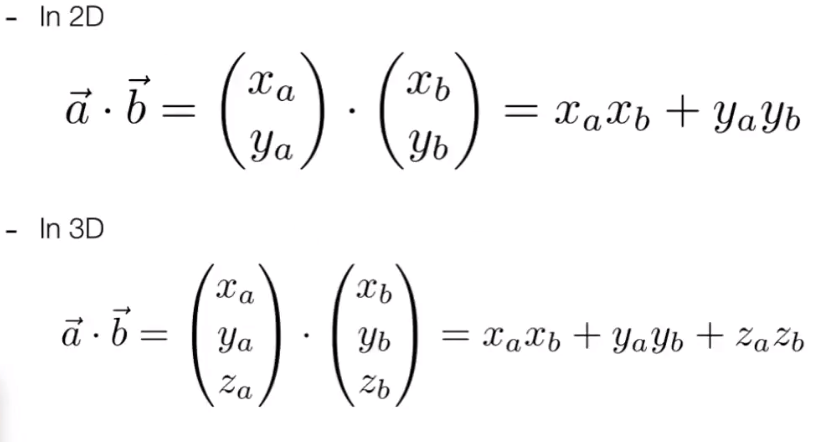
Applications in Graphics:

Find angle between two vectors
- cosine of angle between light source and surface
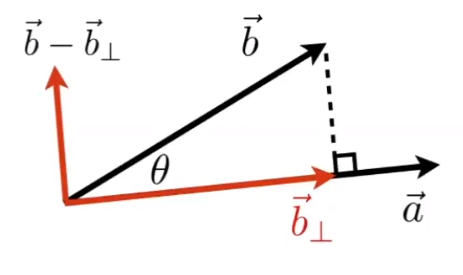
Finding projection of one vector on another
- Measure how close two directions are
- Decompose a vector
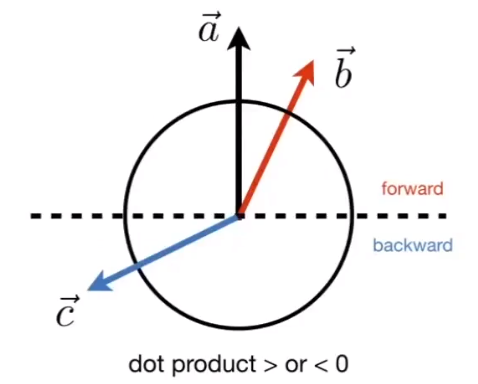
- Determine forward/backward

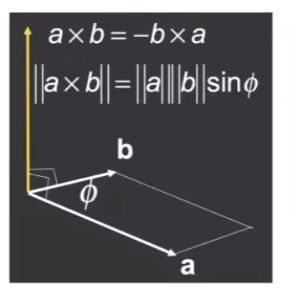
Cross Product

Cross product is orthogonal to two initial vectors
Direction determined by right-hand rule
Useful in constructing coordinate system

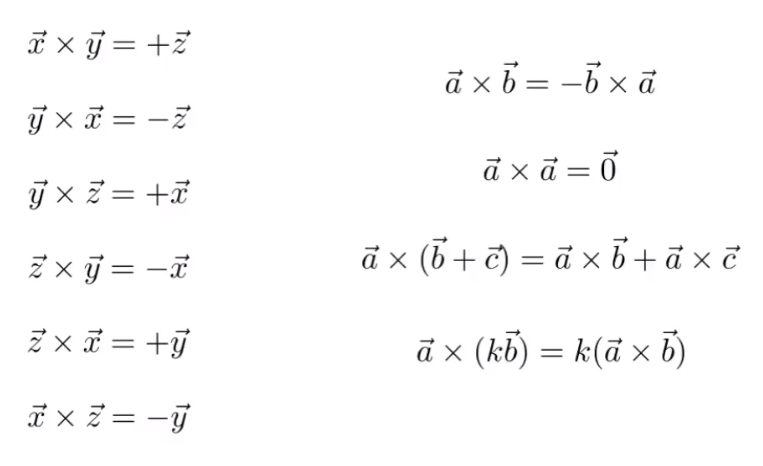
Applications in Graphics:

Determine left/right
Determine inside/outside

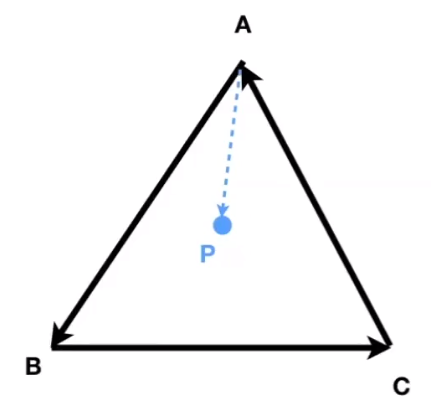
The point P is always in the left (right) of three sides. So P is inside the triangle.

Matrices

In Graphics, pervasively used to represent transformations
- Translation, rotation, shear, scale
Array of numbers
Addition and multiplication by a scalar are trival

Matrix-Matrix Multiplication

columns in A must equal to rows in B
Element (i, j) in the product is the dot product of row i from A and column j from b
Non-commutative
Treawt vector as a column matrix
Key for transforming points

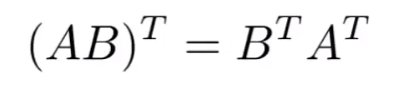
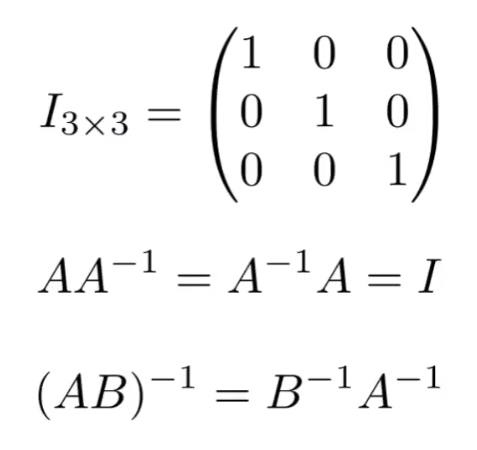
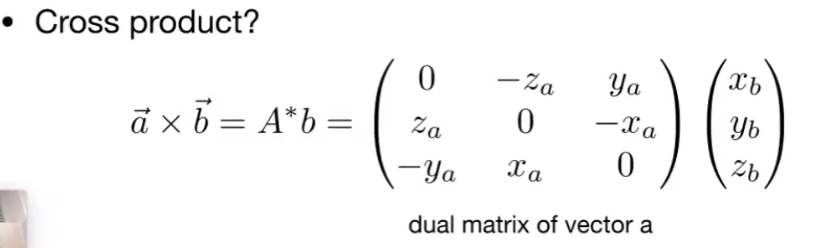
Assignment 0

Question: Given a point \(P=(2,1)\), rotate \(45\) degrees counterclockwise about the origin, then translate \((1, 2)\). Calculate the coordinates of the transformed point.

Solution:

#include<cmath>
#include<iostream>
// Import Eigen Library
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Dense>

using namespace std;
using namespace Eigen;

int main(){
    // Input 2D Point
    Vector2f P(2.f, 1.f);

    // Rotation Angle to Rad conversion
    float angle = 45;
    const float a2r = acos(-1) / 180.0f;
    float rad = angle * a2r;

    // Affine Matrix M
    Matrix3f M;
    M << cos(rad),-sin(rad),1,
          sin(rad),cos(rad),2,
          0,0,1;

    /* 
    M = [
        cos(θ), -sin(θ), X,
        sin(θ), cos(θ), Y,
        0, 0, 1
    ] */
    
    // Temp 3D Point
    Vector3f tmp;
    tmp << P.x(), P.y(), 1.f;

    tmp = M * tmp;
    Vector2f result(tmp.x(), tmp.y());

    cout << result << endl;
    
    return 0;
} 

GAMES101-Review of Linear Algebra

Notes and Ideas