Transformation
2D transformations
- Representing transformations using matrices
- Rotation, scale, shear
Scale Transform
\(x’ = sx, y’ = sy\)
\[\begin{bmatrix} x'\\ y' \end{bmatrix} =\begin{bmatrix} s_x & 0\\ 0 & s_y \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}\]Reflection Matrix
\[\begin{bmatrix} x'\\ y' \end{bmatrix} =\begin{bmatrix} -1 & 0\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}\]Shear Matrix
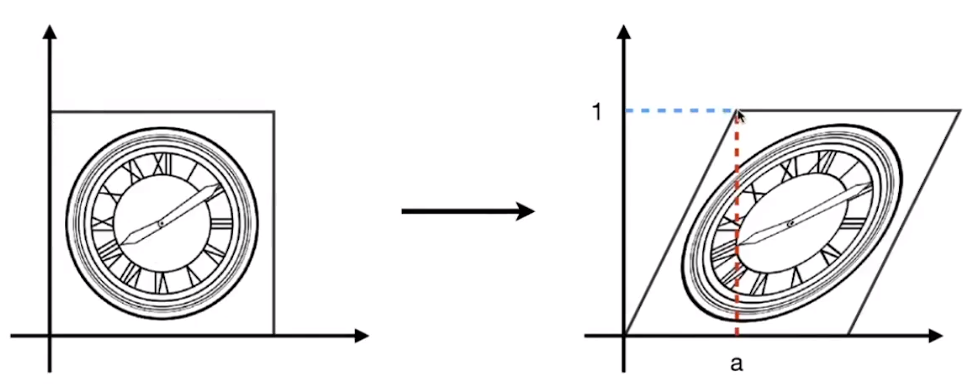
Rotate
Rotation is about the origin \(0, 0\), counter-clockwise by default.
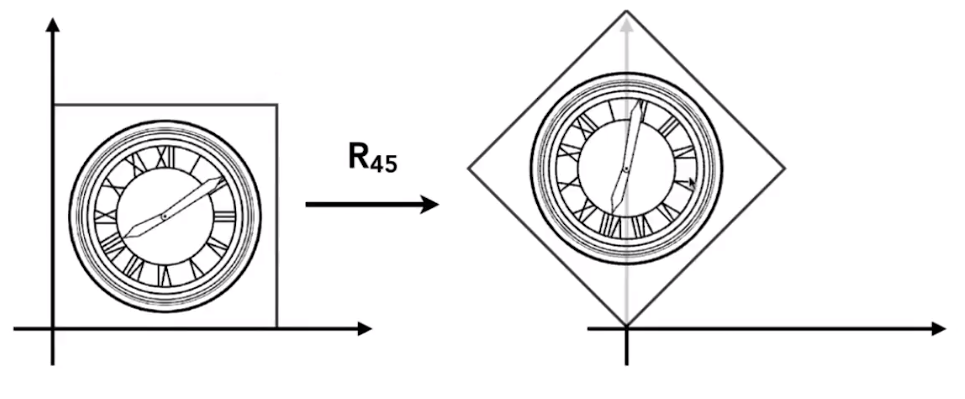
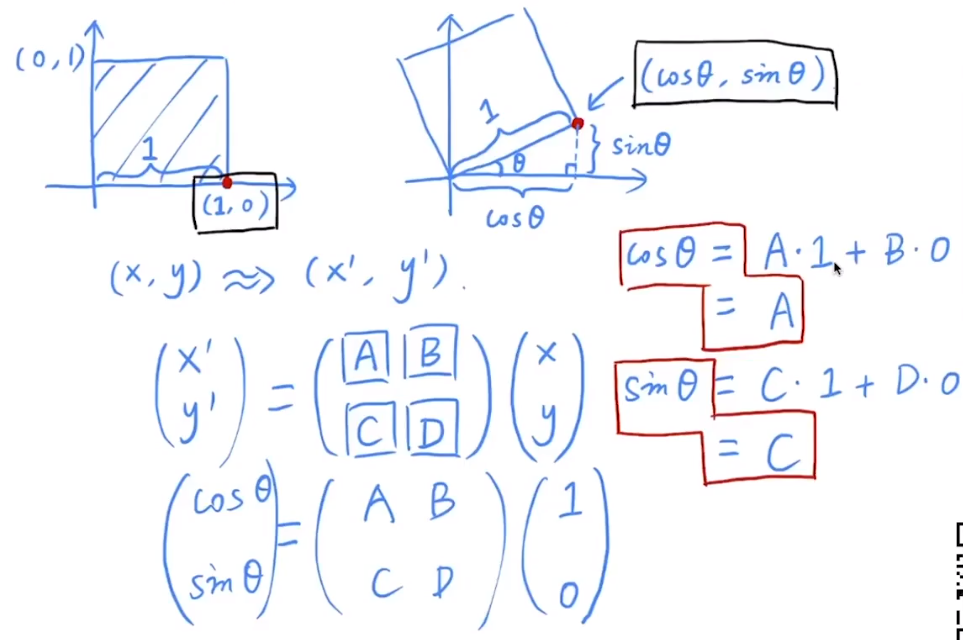
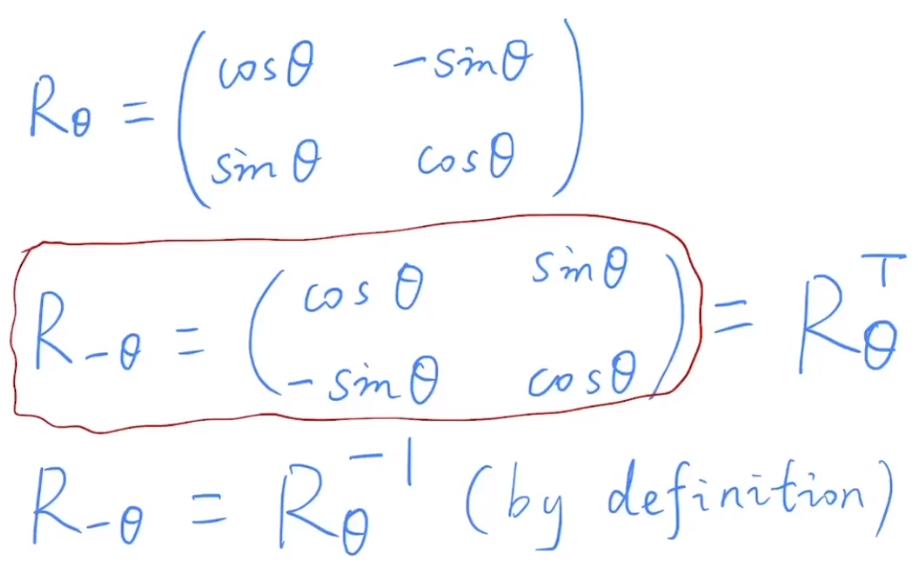
Homogeneous Coordinates
Translation
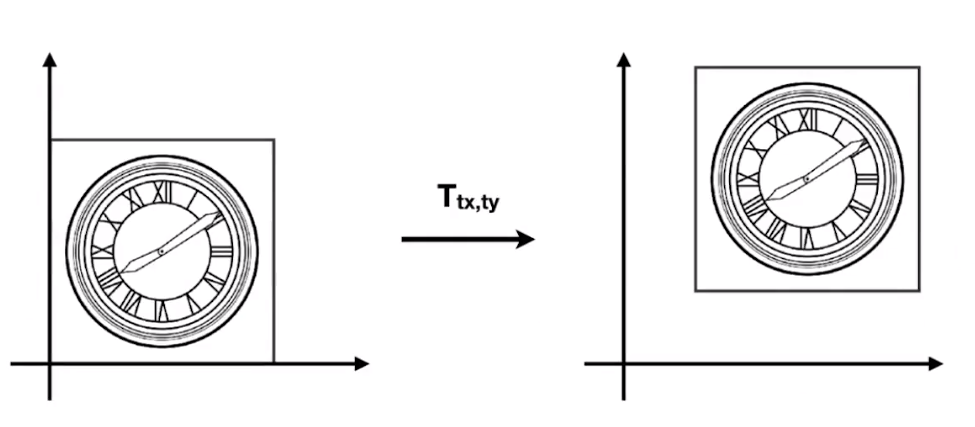
Translation cannot be represented in matrix form.
\[\begin{bmatrix} x'\\ y' \end{bmatrix} =\begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix} +\begin{bmatrix} t_{x}\\ t_{y} \end{bmatrix}\]Translation is not linear transform.
Add a third coordinate in Homogeneous Coordinates:
- 2D point \(=(x,y,1)^\top\)
- 2D vector \(=(x,y,0)^\top\)
Matrix representation of translations:
\[\begin{pmatrix} x'\\ y'\\ w' \end{pmatrix} =\begin{pmatrix} 1 & 0 & t_{x}\\ 0 & 1 & t_{y}\\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} =\begin{pmatrix} x+t_{x}\\ y+t_{y}\\ 1 \end{pmatrix}\]Affine Transformations
Affine map = linear map + translation
\[\begin{bmatrix} x'\\ y' \end{bmatrix} =\begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix} +\begin{bmatrix} t_{x}\\ t_{y} \end{bmatrix}\]Using homogeneous coordinates: \(\begin{pmatrix} x'\\ y'\\ 1 \end{pmatrix} =\begin{pmatrix} a & b & t_{x}\\ c & d & t_{y}\\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ 1 \end{pmatrix}\)
2D transformations

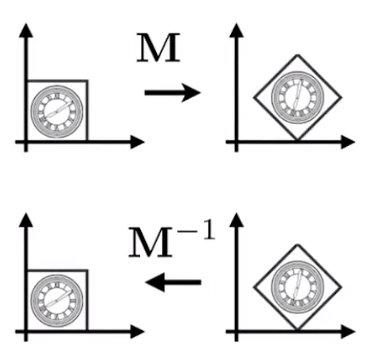
Inverse Transform
\(M^{-1}\) is the inverse of transform \(M\) in both a matrix and geometric sense
Composing Transform
Matrix multiplication is not commutative.
Matrices are applied right to left:
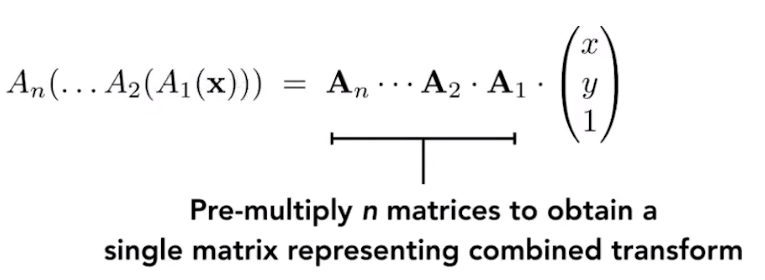
\[T_{( 1,0)} \cdot R_{45} \cdot \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} =\begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} \cos 45\degree & -\sin 45\degree & 0\\ \sin 45 & \cos 45\degree & 0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]Sequence of affine transforms \(A_1, A_2, A_3, \dots\), compose by matrix multiplication.
3D Transforms
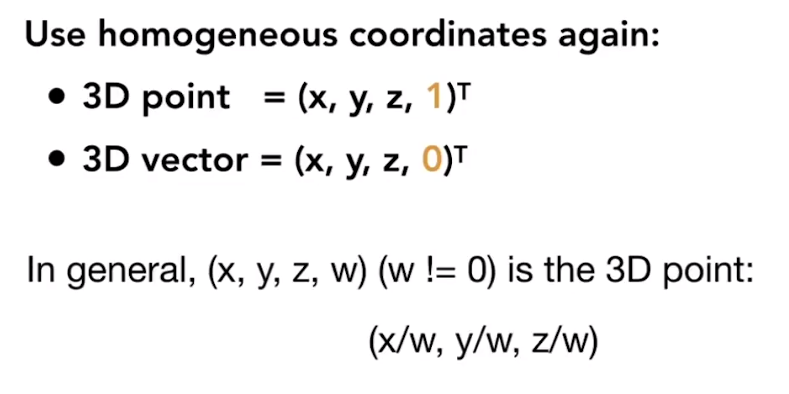

First affine transform, then translation.