Transformation
The inverse of the matrix is equal to its transposed matrix, which we call the orthogonal matrix.
3D Transformations
Use homogeneous coordinates again: 3D point = \((x, y, z, 1)^\top\), 3D vector = \((x,y,z,0)^\top\).
In general, \((x, y, z, w), (w\neq 0)\) is the 3D point \((x/w, y/w, z/w)\).
Using a 4x4 homogeneous coordinates for affine transformations: \(\begin{pmatrix} x'\\ y'\\ z'\\ 1 \end{pmatrix} =\begin{pmatrix} a & b & c& t_{x}\\ d & e & f& t_{y}\\ g & h & i& t_{z}\\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}\)
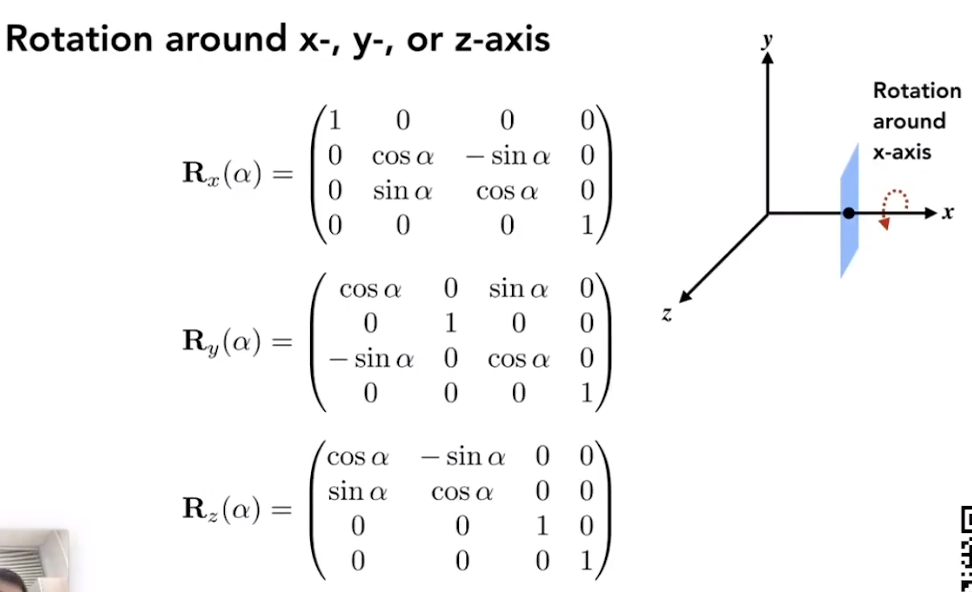
Compose any 3D rotation from \(R_x, R_y, R_z\):
\[R_{xyz}(\alpha, \beta, \gamma) = R_x(\alpha) R_y(\beta) R_z(\gamma)\]Rodrigues’ Rotation Formula
Rotation by angle \(\alpha\) around axis \(n\): \(\mathbb{R}(n, \alpha) = \cos (\alpha) \mathbb{I} + (1 - \cos (\alpha)) \mathbb{n}\mathbb{n}^\top + \sin (\alpha) \begin{bmatrix} 0 & -n_{z} & n_{y}\\ n_{z} & 0 & -n_{x}\\ -n_{y} & n_{x} & 0 \end{bmatrix}\)
Vieweing Transformation
- What is view transformation
- Model transformation (arrange objects)
- View transformation (find a good angle)
- Projection transformation (project to 2D)
- Define the camera first
- Position: \(\vec{e}\)
- Look-at direction: \(\vec{g}\)
- Up direction: \(\vec{t}\), for rotation direction use