Chapter 3. Foundational Components of Neural Networks
Prologue
本章通过介绍构建神经网络的基本思想,如激活函数、损失函数、优化器和监督训练设置,为后面的章节奠定了基础。我们从感知器开始,这是一个将不同概念联系在一起的一个单元的神经网络。感知器本身是更复杂的神经网络的组成部分。
Perceptron: The Simplest Neural Network
最简单的神经网络单元是感知器。感知器在历史上是非常松散地模仿生物神经元的。就像生物神经元一样,有输入和输出,“信号”从输入流向输出,如图所示。
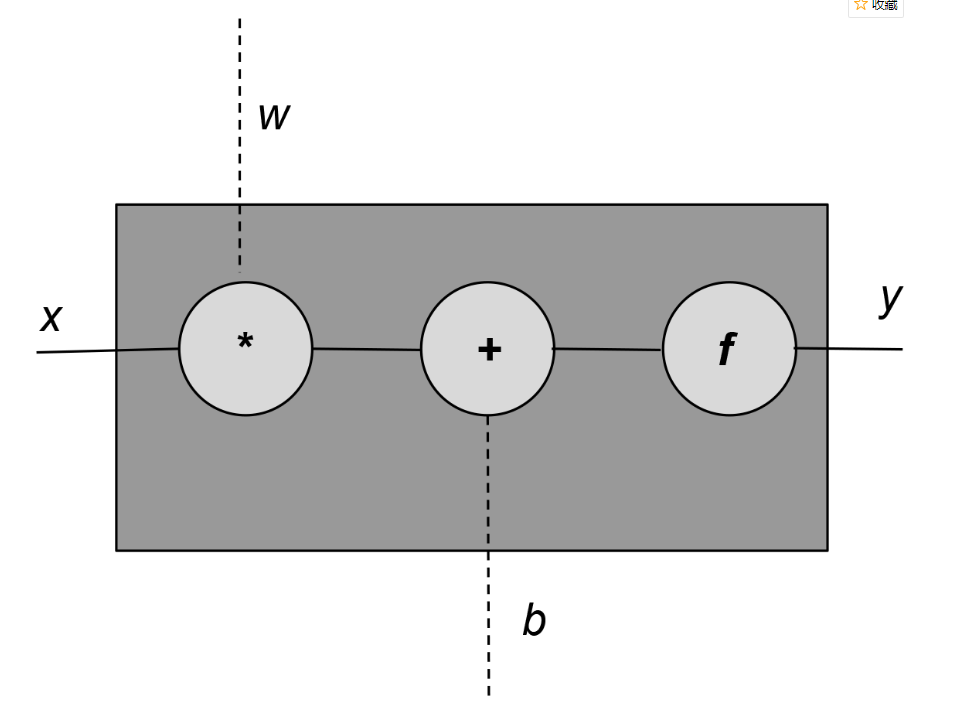
每个感知器单元有一个输入x,一个输出y,和三个“旋钮”(knobs):一组权重w,偏量b,和一个激活函数f。权重和偏量都从数据学习,激活函数是精心挑选的取决于网络的网络设计师的直觉和目标输出。数学上,我们可以这样表示:
通常情况下感知器有不止一个输入。我们可以用向量表示这个一般情况;即,x和w是向量,w和x的乘积替换为点积:
激活函数,这里用f表示,通常是一个非线性函数。
示例展示了PyTorch中的感知器实现,它接受任意数量的输入、执行仿射转换、应用激活函数并生成单个输出。
import torch
import torch.nn as nn
class Perceptron(nn.Module):
""" A Perceptron is one Linear layer """
def __init__(self, input_dim):
"""
Args:
input_dim (int): size of the input features
"""
super(Perceptron, self).__init__()
self.fc1 = nn.Linear(input_dim, 1)
def forward(self, x_in):
"""The forward pass of the Perceptron
Args:
x_in (torch.Tensor): an input data tensor.
x_in.shape should be (batch, num_features)
Returns:
the resulting tensor. tensor.shape should be (batch,)
"""
return torch.sigmoid(self.fc1(x_in)).squeeze()
线性运算\(y=f(\vec{w}^{T}\vec{x} + b)\)称为仿射变换。PyTorch方便地在torch中提供了一个Linear()类。
Act4ivation Functions
激活函数是神经网络中引入的非线性函数,用于捕获数据中的复杂关系。首先,让我们看看一些常用的激活函数。
Sigmoid
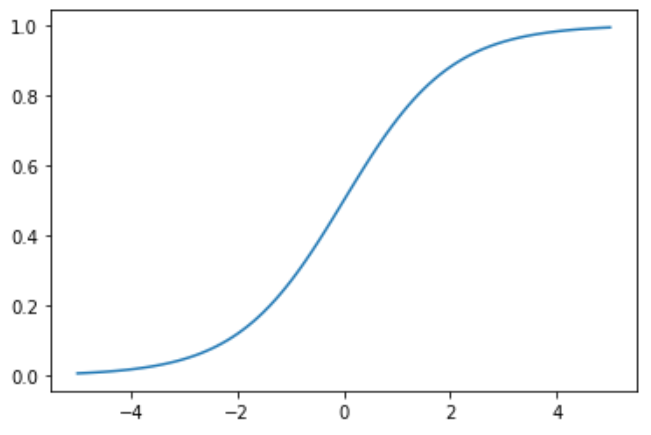
sigmoid是神经网络历史上最早使用的激活函数之一。它取任何实值并将其压缩在0和1之间。数学上,sigmoid的表达式如下:
\[f(x) = \frac{1}{1+e^{-x}}\]从表达式中很容易看出,sigmoid是一个光滑的、可微的函数。Torch将sigmoid实现为Torch .sigmoid(),如示例所示:
import torch
import matplotlib.pyplot as plt
x = torch.range(-5., 5., 0.1)
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
从图中可以看出,sigmoid函数饱和(即,产生极值输出)非常快,对于大多数输入。这可能成为一个问题,因为它可能导致梯度变为零或发散到溢出的浮点值。这些现象分别被称为消失梯度问题和爆炸梯度问题。因此,在神经网络中,除了在输出端使用sigmoid单元外,很少看到其他使用sigmoid单元的情况。在输出端,压缩属性允许将输出解释为概率。
Tanh
tanh激活函数是sigmoid在外观上的不同变体。当你写下tanh的表达式时,这就变得很清楚了:
\[f(x) = tanh x = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]其函数绘制如图所示:
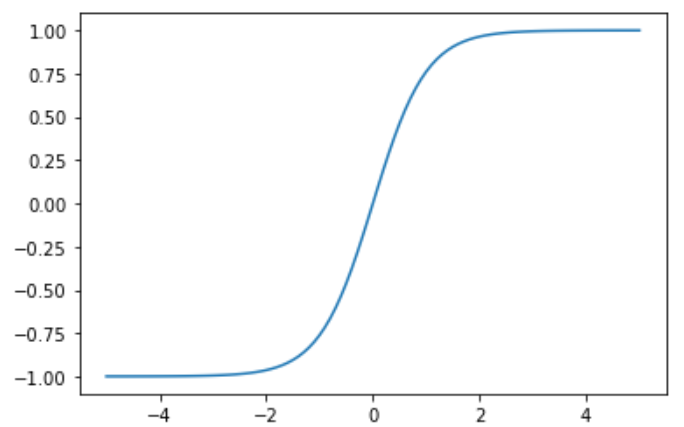
注意双曲正切,像sigmoid,也是一个“压缩”函数,除了它映射一个实值集合从(-∞,+∞)到(-1,+1)范围。
ReLU
ReLU代表线性整流单元。这可以说是最重要的激活函数。事实上,我们可以大胆地说,如果没有使用ReLU,许多最近在深度学习方面的创新都是不可能实现的。对于一些如此基础的东西来说,神经网络激活函数的出现也是令人惊讶的。它的形式也出奇的简单:
\[f(x)=\max(0,x)\]因此,ReLU单元所做的就是将负值裁剪为零。函数绘制如图所示:
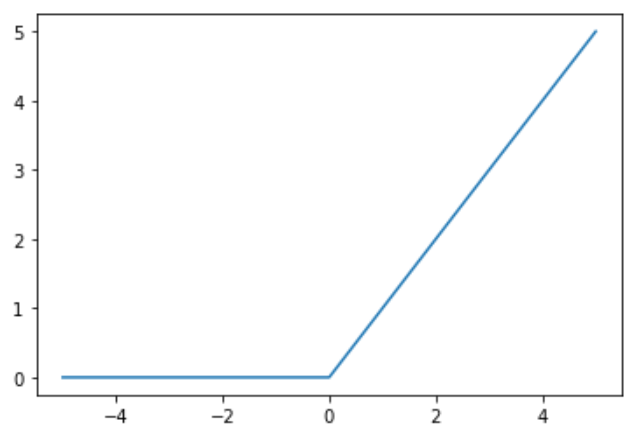
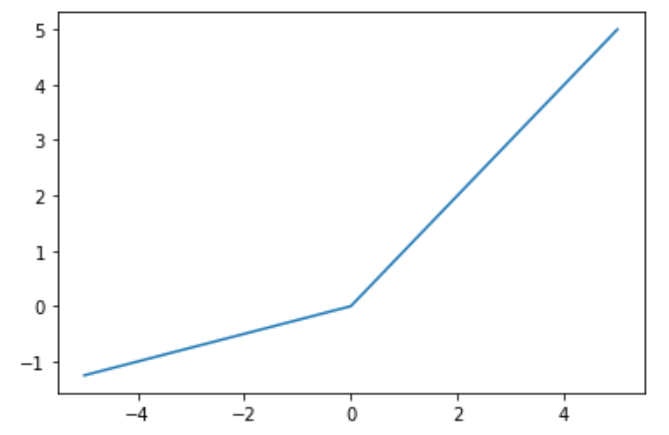
ReLU的裁剪效果有助于消除梯度问题,随着时间的推移,网络中的某些输出可能会变成零,再也不会恢复。这就是所谓的“dying ReLU”问题。为了减轻这种影响,提出了Leaky ReLU或 Parametric ReLU (PReLU)等变体,其中泄漏系数a是一个可学习参数:
\[f(x)=max(x,ax)\]函数绘制如图所示:
Softmax
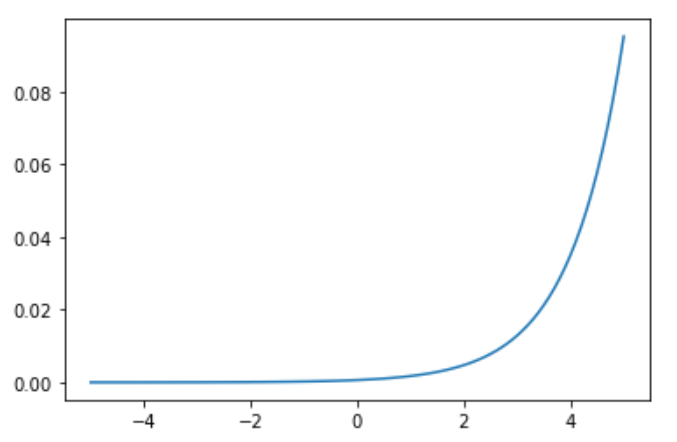
激活函数的另一个选择是softmax。与sigmoid函数类似,softmax函数将每个单元的输出压缩为0到1之间。然而,softmax操作还将每个输出除以所有输出的和,从而得到一个离散概率分布,除以k个可能的类。结果分布中的概率总和为1。这对于解释分类任务的输出非常有用,因此这种转换通常与概率训练目标配对,例如分类交叉熵
\[softmax(x) = \frac{e^{x_i}}{\sum^k_{j=1}e^{x_j}}\]函数绘制如图所示:
Loss Functions
回想一下,一个损失函数truth(y)和预测ŷ作为输入,产生一个实值的分数。这个分数越高,模型的预测就越差。PyTorch在它的nn包中实现了许多损失函数,我们将介绍一些常用的损失函数。
Mean Squared Error Loss
回归问题的网络的输出ŷ和目标y是连续值,一个常用的损失函数的均方误差(MSE)。
MSE就是预测值与目标值之差的平方的平均值。还有一些其他的损失函数可以用于回归问题,例如平均绝对误差(MAE)和均方根误差(RMSE),但是它们都涉及到计算输出和目标之间的实值距离。
import torch
import torch.nn as nn
mse_loss = nn.MSELoss()
outputs = torch.randn(3, 5, requires_grad=True)
targets = torch.randn(3, 5)
loss = mse_loss(outputs, targets)
print(loss)
Categorical Cross-Entropy Loss
分类交叉熵损失(categorical cross-entropy loss)通常用于多类分类设置,其中输出被解释为类隶属度概率的预测。目标y是n个元素的向量,表示所有类的真正多项分布。如果只有一个类是正确的,那么这个向量就是one hot向量。网络的输出ŷ也是一个向量n个元素,但代表了网络的多项分布的预测。分类交叉熵将比较这两个向量(y,ŷ)来衡量损失:
交叉熵和它的表达式起源于信息论,但是为了本节的目的,把它看作一种计算两个分布有多不同的方法是有帮助的。我们希望正确的类的概率接近1,而其他类的概率接近0。
为了正确地使用PyTorch的交叉熵损失,一定程度上理解网络输出、损失函数的计算方法和来自真正表示浮点数的各种计算约束之间的关系是很重要的。具体来说,有四条信息决定了网络输出和损失函数之间微妙的关系。首先,一个数字的大小是有限制的。其次,如果softmax公式中使用的指数函数的输入是负数,则结果是一个指数小的数,如果是正数,则结果是一个指数大的数。接下来,假定网络的输出是应用softmax函数之前的向量。最后,对数函数是指数函数的倒数,和\(\log(\exp (x))\)就等于x。因这四个信息,数学简化假设指数函数和log函数是为了更稳定的数值计算和避免很小或很大的数字。这些简化的结果是,不使用softmax函数的网络输出可以与PyTorch的交叉熵损失一起使用,从而优化概率分布。然后,当网络经过训练后,可以使用softmax函数创建概率分布.
import torch
import torch.nn as nn
ce_loss = nn.CrossEntropyLoss()
outputs = torch.randn(3, 5, requires_grad=True)
targets = torch.tensor([1, 0, 3], dtype=torch.int64)
loss = ce_loss(outputs, targets)
print(loss)
Binary Cross-Entropy
有时,我们的任务包括区分两个类——也称为二元分类。在这种情况下,利用二元交叉熵损失是有效的。
在示例中,我们使用表示网络输出的随机向量上的sigmoid激活函数创建二进制概率输出向量。接下来,ground truth被实例化为一个0和1的向量。最后,利用二元概率向量和基真值向量计算二元交叉熵损失。
bce_loss = nn.BCELoss()
sigmoid = nn.Sigmoid()
probabilities = sigmoid(torch.randn(4, 1, requires_grad=True))
targets = torch.tensor([1, 0, 1, 0], dtype=torch.float32).view(4, 1)
loss = bce_loss(probabilities, targets)
print(probabilities)
print(loss)
Diving Deep into Supervised Training
有监督学习需要以下内容:模型、损失函数、训练数据和优化算法。监督学习的训练数据是观察和目标对,模型从观察中计算预测,损失衡量预测相对于目标的误差。训练的目的是利用基于梯度的优化算法来调整模型的参数,使损失尽可能小。
在本节的其余部分中,我们将讨论一个经典的玩具问题:将二维点划分为两个类中的一个。直观上,这意味着学习一条直线(称为决策边界或超平面)来区分类之间的点。我们一步一步地描述数据结构,选择模型,选择一个损失,建立优化算法,最后,一起运行它。
Constructing Toy Data
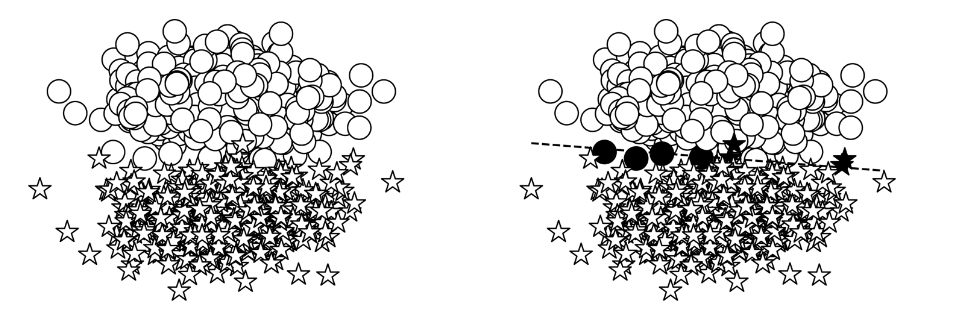
在机器学习中,当试图理解一个算法时,创建具有易于理解的属性的合成数据是一种常见的实践。在本节中,我们使用“玩具”任务的合成数据——将二维点分类为两个类中的一个。为了构建数据,我们从xy平面的两个不同部分采样点,为模型创建了一个易于学习的环境。
如图所示。模型的目标是将星星⋆作为一个类,◯作为另一个类。这可以在图的右边看到,线上面的东西和线下面的东西分类不同。
def get_toy_data(batch_size, left_center=LEFT_CENTER, right_center=RIGHT_CENTER):
x_data = []
y_targets = np.zeros(batch_size)
for batch_i in range(batch_size):
if np.random.random() > 0.5:
x_data.append(np.random.normal(loc=left_center))
else:
x_data.append(np.random.normal(loc=right_center))
y_targets[batch_i] = 1
return torch.tensor(x_data, dtype=torch.float32), torch.tensor(y_targets, dtype=torch.float32)
Choosing a Model
我们在这里使用的模型是在本章开头介绍的:感知器。感知器是灵活的,因为它允许任何大小的输入。在典型的建模情况下,输入大小由任务和数据决定。在这个玩具示例中,输入大小为2,因为我们显式地将数据构造为二维平面。对于这个两类问题,我们为类指定一个数字索引:0和1。字符串的映射标签⋆和◯类指数是任意的,只要它在数据预处理是一致的,训练,评估和测试。
该模型的另一个重要属性是其输出的性质。由于感知器的激活函数是一个sigmoid,感知器的输出为数据点x为class 1的概率,即\(P(y = 1 |
x)\)。 |
Converting the Probabilities to Discrete Classes
对于二元分类问题,我们可以输出概率转换成两个离散类通过利用决策边界,δ。如果预测的概率P(y = 1 | x)>δ,预测类是1,其它类是0。通常,这个决策边界被设置为0.5,但是在实践中,您可能需要优化这个超参数(使用一个评估数据集),以便在分类中获得所需的精度。
Choosing a Loss Function
在准备好数据并选择了模型体系结构之后,在有监督的培训中还可以选择另外两个重要组件:损失函数和优化器。在模型输出为概率的情况下,最合适的损失函数是基于熵的交叉损失。对于这个玩具数据示例,由于模型产生二进制结果,我们特别使用BCE损失。
Chossing an Optimizer
在这个简化的监督训练示例中,最后的选择点是优化器。当模型产生预测,损失函数测量预测和目标之间的误差时,优化器使用错误信号更新模型的权重。最简单的形式是,有一个超参数控制优化器的更新行为。这个超参数称为学习率,它控制错误信号对更新权重的影响。学习速率是一个关键的超参数,你应该尝试几种不同的学习速率并进行比较。较大的学习率会对参数产生较大的变化,并会影响收敛性。学习率过低会导致在训练过程中进展甚微。
PyTorch库为优化器提供了几种选择。随机梯度下降法(SGD)是一种经典的选择算法,但对于复杂的优化问题,SGD存在收敛性问题,往往导致模型较差。当前首选的替代方案是自适应优化器,例如Adagrad或Adam,它们使用关于更新的信息。在下面的例子中,我们使用Adam。对于Adam,默认的学习率是0.001。对于学习率之类的超参数,总是建议首先使用默认值,除非您从论文中获得了需要特定值的秘诀。
import torch.nn as nn
import torch.optim as optim
input_dim = 2
lr = 0.001
perceptron = Perceptron(input_dim=input_dim)
bce_loss = nn.BCELoss()
optimizer = optim.Adam(params=perceptron.parameters(), lr=lr)
Putting It Together: Gradient-Based Supervised Learning
学习从计算损失开始;也就是说,模型预测离目标有多远。损失函数的梯度,反过来,是参数应该改变多少的信号。每个参数的梯度表示给定参数的损失值的瞬时变化率。实际上,这意味着您可以知道每个参数对损失函数的贡献有多大。直观上,这是一个斜率,你可以想象每个参数都站在它自己的山上,想要向上或向下移动一步。基于梯度的模型训练所涉及的最简单的形式就是迭代地更新每个参数,并使用与该参数相关的损失函数的梯度。
让我们看看这个梯度步进(gradient-steeping)算法是什么样子的。首先,使用名为zero_grad()的函数清除当前存储在模型(感知器)对象中的所有信息,例如梯度。然后,模型计算给定输入数据 x_data的输出y_pred。接下来,通过比较模型输出y_pred和预期目标y_target来计算损失。这正是有监督训练信号的有监督部分。PyTorch损失对象(criteria)具有一个名为bcakward()的函数,该函数迭代地通过计算图向后传播损失,并将其梯度通知每个参数。最后,优化器(opt)用一个名为step()的函数指示参数如何在知道梯度的情况下更新它们的值。
整个训练数据集被划分成多个batch。例如,训练数据可能有数百万个,而小批数据可能只有几百个。梯度步骤的每一次迭代都在一批数据上执行。名为batch_size的超参数指定批次的大小。由于训练数据集是固定的,增加批大小会减少批的数量。在多个批处理(通常是有限大小数据集中的批处理数量)之后,训练循环完成了一个epoch。epoch是一个完整的训练迭代。如果每个epoch的批数量与数据集中的批数量相同,那么epoch就是对数据集的完整迭代。模型是为一定数量的epoch而训练的。要训练的epoch的数量对于选择来说不是复杂的,但是有一些方法可以决定什么时候停止,我们稍后将讨论这些方法。
如下例所示,受监督的训练循环因此是一个嵌套循环:数据集或批处理集合上的内部循环,以及外部循环,后者在固定数量的epoches或其他终止条件上重复内部循环。
# each epoch is a complete pass over the training data
for epoch_i in range(n_epochs):
# the inner loop is over the batches in the dataset
for batch_i in range(n_batches):
# Step 0: Get the data
x_data, y_target = get_toy_data(batch_size)
# Step 1: Clear the gradients
perceptron.zero_grad()
# Step 2: Compute the forward pass of the model
y_pred = perceptron(x_data, apply_sigmoid=True)
# Step 3: Compute the loss value that we wish to optimize
loss = bce_loss(y_pred, y_target)
# Step 4: Propagate the loss signal backward
loss.backward()
# Step 5: Trigger the optimizer to perform one update
optimizer.step()
Auxiliary Training Concepts
基于梯度监督学习的核心概念很简单:定义模型,计算输出,使用损失函数计算梯度,应用优化算法用梯度更新模型参数。然而,在训练过程中有几个重要但辅助的概念。
Evaluation Metrics
核心监督训练循环之外最重要的部分是使用模型从未训练过的数据来客观衡量性能。模型使用一个或多个评估指标进行评估。在自然语言处理(NLP)中,存在多种评价指标。最常见的,也是我们将在本章使用的,是准确性。准确性仅仅是在训练过程中未见的数据集上预测正确的部分。
Splitting the Dataset
一定要记住,最终的目标是很好地概括数据的真实分布。我们用有限的样本作为训练数据。我们观察有限样本中的数据分布这是真实分布的近似或不完全图像。如果一个模型不仅减少了训练数据中样本的误差,而且减少了来自不可见分布的样本的误差,那么这个模型就比另一个模型具有更好的通用性。当模型致力于降低它在训练数据上的损失时,它可以过度适应并适应那些实际上不是真实数据分布一部分的特性。
要实现这一点,标准实践是将数据集分割为三个随机采样的分区,称为训练、验证和测试数据集,或者进行k-fold交叉验证。分成三个分区是两种方法中比较简单的一种,因为它只需要一次计算。您应该采取预防措施,确保在三个分支之间的类分布保持相同。换句话说,通过类标签聚合数据集,然后将每个由类标签分隔的集合随机拆分为训练、验证和测试数据集,这是一种很好的实践。一个常见的分割百分比是预留70%用于培训,15%用于验证,15%用于测试。
重要的是只使用训练数据更新模型参数,在每个epoch结束时使用验证数据测量模型性能,在所有的建模选择被探索并需要报告最终结果之后,只使用测试数据一次。这最后一部分是极其重要的,因为更多的机器学习工程师在玩模型的性能测试数据集,他们是偏向选择测试集上表现得更好。当这种情况发生时,它是不可能知道该模型性能上看不见的数据没有收集更多的数据。
使用k-fold交叉验证的模型评估与使用预定义分割的评估非常相似,但是在此之前还有一个额外的步骤,将整个数据集分割为k个大小相同的fold。其中一个fold保留用于评估,剩下的k-1fold用于训练。通过交换出计算中的哪些fold,可以重复执行此操作。因为有k个fold,每一个fold都有机会成为一个评价fold,并产生一个特定于fold的精度,从而产生k个精度值。最终报告的准确性只是具有标准差的平均值。k-fold评估在计算上是昂贵的,但是对于较小的数据集来说是非常必要的,对于较小的数据集来说,错误的分割可能导致过于乐观(因为测试数据太容易了)或过于悲观(因为测试数据太困难了)。
Knowing When to Stop Training
之前的例子训练了固定次数的模型。正确度量模型性能的一个关键功能是使用该度量来知道何时应该停止训练。最常用的方法是使用启发式方法,称为早期停止(early stopping)。早期停止通过跟踪验证数据集上从一个epoch到另一个epoch的性能并注意性能何时不再改进来的工作。然后,如果业绩继续没有改善,训练将终止。在结束训练之前需要等待的时间称为耐心。一般来说,模型停止改进某些数据集的时间点称为模型收敛的时间点。在实际应用中,我们很少等待模型完全收敛,因为收敛是耗时的,而且会导致过拟合。
Finding the Right Hyperparameters
我们在前面了解到,参数(或权重)采用优化器针对称为minibatch的固定训练数据子集调整的实际值。超参数是影响模型中参数数量和参数所取值的任何模型设置。有许多不同的选择来决定如何训练模型。这些选择包括选择一个损失函数、优化器、优化器的学习率、层大小、早停止,和各种正规化决策。
Regularization
深度学习(以及机器学习)中最重要的概念之一是正则化。正则化的概念来源于数值优化理论。回想一下,大多数机器学习算法都在优化损失函数,以找到最可能解释观测结果(即,产生的损失最少)。对于大多数数据集和任务,这个优化问题可能有多个解决方案(可能的模型)。那么我们(或优化器)应该选择哪一个呢?
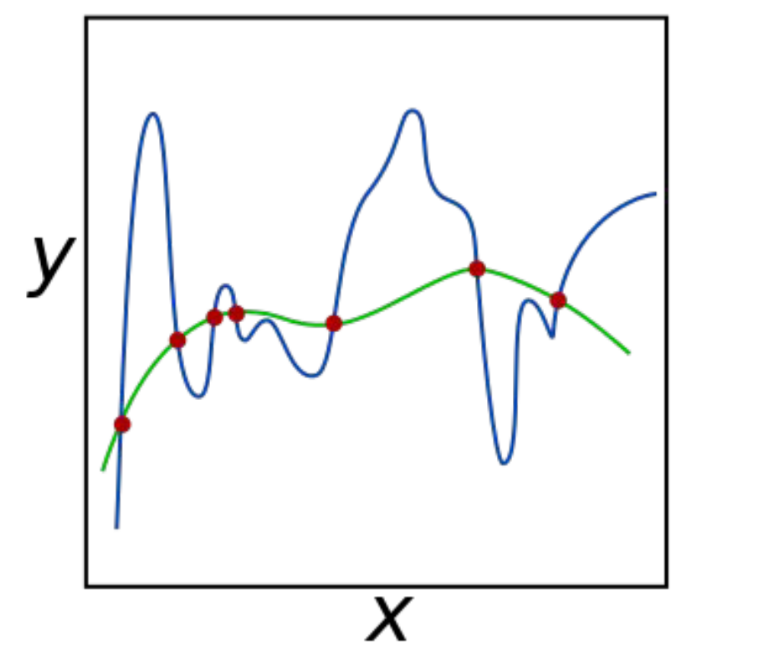
两条曲线都能够拟合这些点,但哪一条是不太可能的解释呢?通过求助于奥卡姆剃刀,我们凭直觉知道一个简单的解释比复杂的解释更好。这种机器学习中的平滑约束称为L2正则化。在PyTorch中,您可以通过在优化器中设置weight_decay参数来控制这一点。weight_decay值越大,优化器选择的解释就越流畅;也就是说,L2正则化越强。
除了L2,另一种流行的正则化是L1正则化。L1通常用来鼓励稀疏解;换句话说,大多数模型参数值都接近于零。