Origin: Crystal Nets as Graphs
Crystal Nets as Graphs
Molecular topology is a graph
Atom (vertices) joined by bonds (edges).
Crystals e.g. diamond have topology specified by an infinite periodic graph.
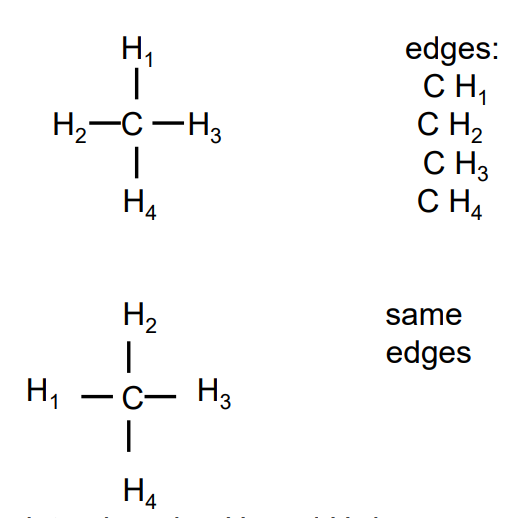
Interchanging \(H_1\) and \(H_2\) is an automorhism of the graph.
- Graph is an abstract mathematical object.
- Network is a real thing.
Graph consists of vertices and edges connect two vertices.
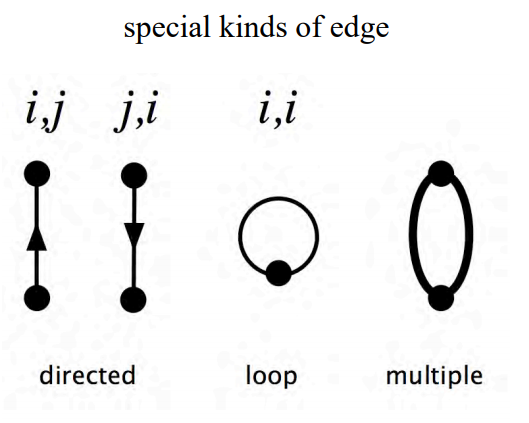
A faithful embedding is a realization in which edges are finite and do not intersect.
Graphs which admit a 2-dimensional faithful embeding are planar.
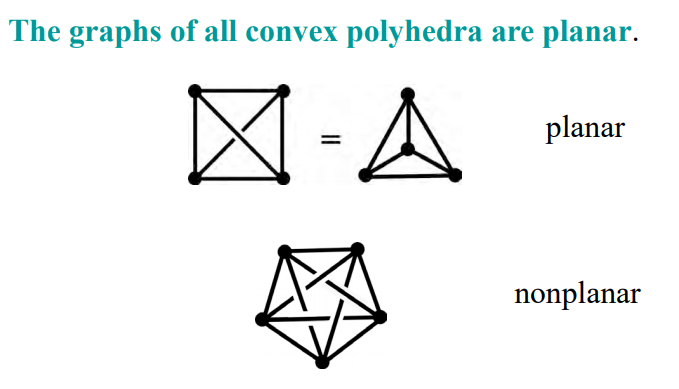
Sometimes we want to distinguish the abstract graph with vertices and edges from an embedding with nodes and links.
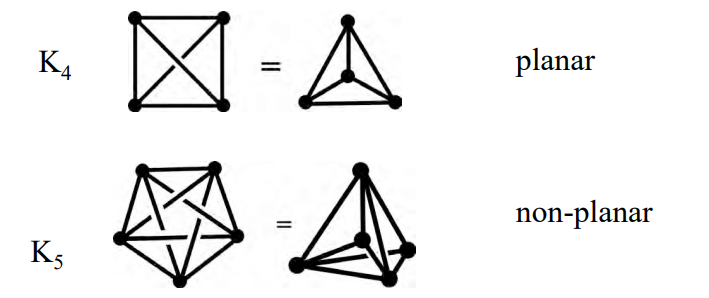
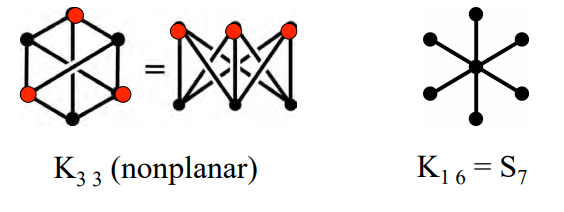
Complete graphs: every vertex linked to every other vertex.
Complete bipartite graph \(K_{mn}\): Two sets of vertices \(m\) in one set and \(n\) in the other all \(m\) linked only to all \(n\).
The graph \(K_{1n}\) is the same as the star graph \(S_{n+1}\).
Bipartite two classes of vertex. Vertices in each class linked only to the vertices of the other class.
Tree has no cycles (closed paths).
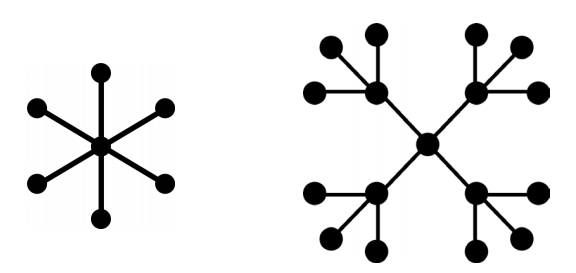
Regular graph has the same number, n, of edges meeting at each vertex. The number of edges is \(n/2\) time the number of vertices.
Symmetric graph: vertex and edge transitive
semisymmetric graph: edge but not vertex transitive
girth: length of shortest cycle
Transitivity
Vertex transitive (“uninodal”) = one kind of vertex (all vertices related by symmetry)
Vertex 2-transitive (“binodal”) = two kinds of vertex
Edge transitive = one kind of edge
A connected graph has a continuous path between every pair of vertices.