Abstract
Current generative approaches exhibit a significant challenge as they do not ensure that the proposed molecular structures can be feasibly synthesized nor do they provide the synthesis routes of the proposed small molecules, there by seriously limiting their practical applicalibity. Policy Gradient for Forward Synthesis (PGFS), that addresses this challenge by embedding the concept of synthetic accessibility directly into the de novo drug design system.
Introduction
In the last decade, deep generative models such as GANs and VAEs have emerged as promising new techniques to design novel molecules with desirable properties. However, the majority of de novo drug design methodologies do not explicitly account for synthetic feasibility, and thus cannot ensure whether the generated molecules can be produced in the physical world.
Directly embedding synthetic knowledge into de novo drug design would allow us to constrain the search to synthetically-accessible routes and theoretically guarantee that any molecule proposed by the algorithm can be easily produced. Policy Gradient for Forward Synthesis (PGFS) that treats the generation of a molecular structure as a sequential decision process of selecting reactant molecules and reation transformations in a linear synthetic seqence. The agent learns to select the best set of reactants and reactions to maximize the task-specific desired properties of the product molecule, i.e., where the choice of reactants is considered an action, and a product molecule is a state of the system obtained through a trajectory composed of the chosen chemical reactions.
The primary contribution of this work is the development of a RL framwork able to cope with the vast discrete action space of mlti-step virtual chemical synthesis and bias of multi-step virtual chemical structures that maximize a black-box objective function, generating a full synthetic route in the process. We define the problem of de novo drug design via forward synthesis as a Markov decision process in chemical reaction space. We propose to search in a continuous action space using a relevant feature space for reactants rather than a discrete space to facilitate the learning of agent.
Training is guided by rewards which correspond to the predicted properties of the resulting molecule relative to the desired properties.
Related Work
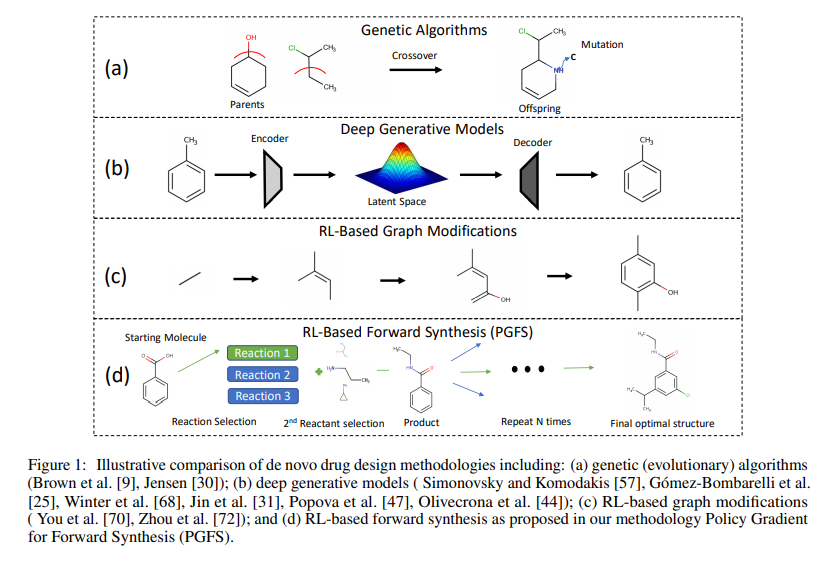
Genetic Algorithms
Genetic algorithms (GA) have been used for many decades to generate ad optimize novel chemical structures. They represent one of the most straightfoward and simple approaches for de novo drug design and can perform on-par with complex generative models across populaar benchmark tasks. Existing implementations of GA for de novo generation can only account for synthetic feasibility through the inroduction of a heuristic scoring functions as poart of the reward function. As a result, they need a separate model for retrosynthesis or manual evaluation by an expert upon identifying a structure with desired properties.
Deep Generative Models
Many recent studies highlight applications of deep generative systems in multi-objective optimization of chemical structures. While these approach have provided valuable techniques for optimizing various types of molecular properties in single- and multiple-objective settings, they exhibit the same challenges in synthetic feasibility as GA.
RL-Based Graph Modification Models
Recently proposed reforcement learning based algorithms to iteratively modify a molecule by adding and removing atoms, bonds or molecular subgraphs. In such setups, the constructed molecure \(M_t\), represents the state at time step \(t\). The state at time step 0 can be a single atom like carbon or it can be completely null. The agent is trained to pick actions that would optimize the properties of the generated molecules. While these methods have achieved promising results, they do not guarantee synthetic feasibility.
Forward Synthesis Models
The generation of molecules using forward synthesis is the most straightforward way to deal with the problem of synthetic accessibility.
Methods
Reinforcement Learning
To explore the large chemical space efficiently and maintain the ability to generate diverse compounds, we propose to consider a molecule as a sequence of unimoleclar or bimolecular reactions applied to an initial molecule. PGFS learns to select the best set of commercially available reactants and reaction templates that maximize the rewards associated with the properties of the product molecule. The state of the system at each step corresponds to a product molecule and the rewards are computed according to the properties of the product.
Futhermore, the method decomposes actions of synthetic steps in two sub-actions. A reaction template is first selected and is followed by the selection of a reactant compatible with it. This hierarchical decomposition considerably reduces the size of the action space in each of the time steps in contrast to simultaneously picking a reactant and reaction type.
However, this formulation still poses challenges for current RL algorithms owing to the large action space. There are tens of thousands of possible reactants for each given molecule and reaction template. As a result, we propose to adapt algorithms corresponding to continuous action space and map continuous embeddings to discrete molecular structures by looking up the nearest molecules in this representation space via a kNN algorithm. In this work, we leverage a TD3 algorithm along with the kNN approach.
There are three key difference with this work:
- The actor module includes two learnable network to compute two levels of actions
- We do not use a critic network in the forward propagation, and include the kNN computation as part of the environment. Thus, the continuous output of the actor module reflects the true actions
- We leverage the TD3 algorithm which has been shown to be better than DPG on several RL tasks.
Overview
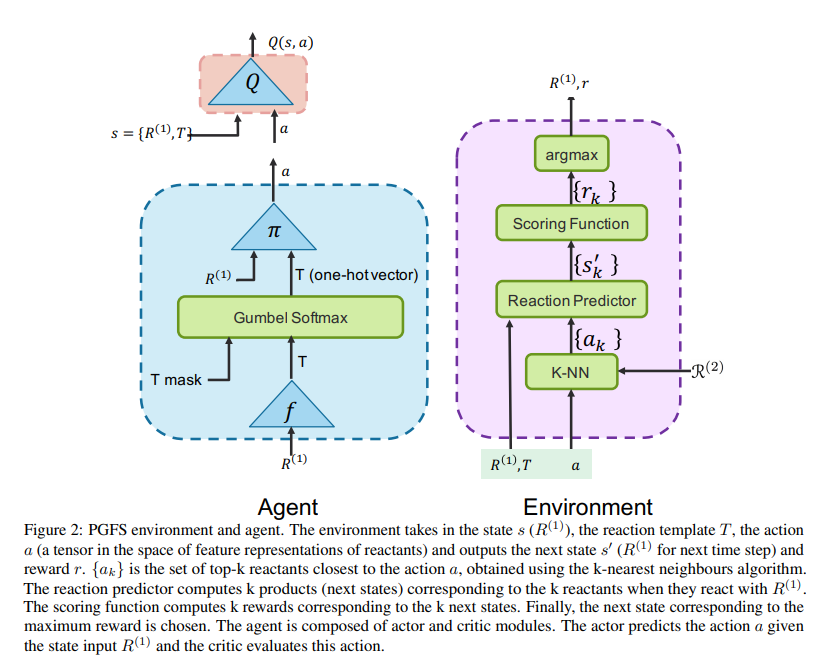
The pipeline is setup in such a way that at every time step \(t\), a reactant \(R_t^{(2)}\) is selected to react with the existing molecule \(R_t^{(1)}\) to yield the product \(R_{t+1}^{1}\) which is the molecule for the next time step.
\(R_t^{(1)}\) is considered as the current state \(s_t\) and out agent chooses an action \(a_t\) that is further used in computing \(R_t^{(2)}\). The product \(R_{t+1}^{(1)}\) (which is considered as the next state \(s_{t+1}\)) is determined by the environment based on the two reactants \(R_t^{(1)}\) and \(R_t^{(2)}\).
At the very initial time step, we randomly sample the initial molecule \(R_0^{(1)}\) from the list of all available reactants. To overcome the limitation of large discrete action space where there are over a hundred thousand possible second reactants, we introduce an intermediate action which reduce the space of reactants considered by choosing a reaction template. Reaction templates, encoded in the SMARTS language, define allowable chemical transformations according to subgraph matching rules. They can be applied deterministically to sets of reactant molecules to propose hypothetical product molecules using cheminformatics tools like RDKit.
One of the reactants is the state \(s_t\) while the other reactant is later selected. Since the required substructure of \(R_t^{(2)}\) that can participate in the reaction and of the state \(s_t\) is determined by the choice of the reaction template, the action space comprising the space of all \(R^{(2)}\)s becomes constrained to those reactants which contain this particular substructure.
We also enforce the additional constraint of having this substructure present only once in the structure. Pairs of reactants associated with different templates that can participate in several different reactions are also forbidden. When multiple products are still possible, one of tem is selected randomly. Even with the previous constraints, there can be tens of thousads of reactants at each step, and thus represents a challenge for tranditional RL algorithms. Thus, we formulate a novel MDP involving a continuous action space.
The agent comprises three learnable networks \(f, \pi\), and \(Q\). In terms of the actor-critic framework, our actor module \(\Pi\) comprises \(f\) and \(\pi\) networks and the criti is composed of the \(Q\) network that estimates the Q-value of the state-action pair.
At any time step \(t\), the input to the actor module is the state \(s_t(R_t^{(1)})\) and the output is the action \(a_t\) which is a tensor defined in the feature representation space of all initial reactants \(R^{(2)}\). The \(f\) network predicts the best reaction template \(T_t\) given the current state \(s_t(R_t^{(1)})\). Using the best reaction template \(T_t\) and \(R_t^{(1)}\) as inputs, the \(\pi\) network computes the action \(a_t\). The environment takes the state \(s_t\), best reaction template \(T_t\), and action \(a_t\) as inputs and computes the reward \(r_t\), next state \(s_{t+1}\) and a boolean to determine whether the episode has ended.
It first chooses \(k\) reactants from the set \(R^{(2)}\) corresponding to the k-closest embeddings to the action \(a\) using the kNN technique in which we pre-compute feature representations for all reactants. Each of these \(k\) actions are then passed through a reaction predictor to obtain the corresponding k products.
The rewards associated with the products are computed using a scoring function. The reward and product corresponding to the maximum reward are returned. The state \(s_t\), best template \(T_t\), action \(a_t\), next state \(s_{t+1}\), reward \(r_t\) are stored in the reply memory buffer. The episode terminates when either the masimum number of reaction steps is reached or when the next state has no valid templates.
In our experiments, we have 15 unimolecular and 82 bimolecular reaction templates. The unimolecular templates do not require selection of an \(R^{(2)}\), and hence for such cases we directly obtain the product using \(R_t^{(1)}\) and the selected \(T_t\).
During initial phases of the training, it is important to note that the template chosen by the \(f\) network might be invalid. To overcome this issue and to ensure the gradient propagation through the \(f\) network, we first multiply the template T with the template mask \(T_{mask}\) and then use Gumbel softmax to obtain the best template:
\[T = T \odot T_{mask}\] \[T = GumbleSoftmax(T, \tau)\]where \(\tau\) is the temperature parameter that is slowly annealed from 1.0 to 0.1.
Training Paradigm
The learning agent can be trained using any policy gradient algorithm applicable for continuous action spaces. Thus, we call our algorithm “Poly Gradient for Forward Synthesis (PGFS)”. After sampling a random minibatch of \(N\) transitions from the buffer, the actor and critic modules are updated as follows: The critic (\(Q\)-network) is updated using the one-step TD update rule as:
\[y_i=r_i + \gamma Q'(s_{i+1}, \Pi '(s_{i+1}))\]where, \(Q’\) and \(\Pi ‘\) are the target critic and actor networks respectively, i.e., they are a copy of the original networks but they do not update their parameters during gradient updates. \(y_i) is the one-step TD target, \(r_i\) is the immediate reward and \(s_i\) constitutes the state at the time step \(t\). \(s_{i+1}\) forms the state at next time step. The critic loss is then:
\[L = \frac{1}{N} \sum_i (y_i - Q(s_i, a_i))^2\]and the parameters of the Q network are updated via back propagation of the critic loss. The goal of the actor module is to maximize the overall return achieved over the given initial distribution of states by following the actions determined by the actor module. The Q network can be seen as an approximation to this overall return. Thus, the actor should predict actions that maximize the \(Q(s, a)\) values predicted by Q network, i.e., \(\max Q(s, \Pi (s))\), or \(\min Q(s, \Pi (s))\). Thus, \(-Q(s, \Pi (s))\) constitutes the actor loss. Consequently, the parameters of the actor module (of \(f\) and \(\pi\) networks) are updated towards reducing that loss.
However, the convergence of returns observed is slow. The fast training technique is provided:
First, we smooth the target policy by adding a small amount of clipped random noises to the action.
\[\tilde{a} = a+\epsilon; \epsilon ~ clip(N(0, \tilde{\sigma}), -c, c)\]We use a double Q-learning strateg comprising two critics, but only consider the minimum of two critics for computing the TD target:
\[y = r + \gamma \min_{i=1, 2} Q_i (s', \Pi (s'))\]Futher, we make delayed updates (once every two critic updates) to the actor module and target networks.
To speed up the convergence of the \(f\) network, we also minimize the cross entropy between the output of the \(f\) network, and the corresponding template \(T\) obtained for the reactant \(R^{(1)}\).
