Model-Free Prediction

Introduction

上一节讲的是在已知模型的情况下，如何去解决一个马尔科夫决策过程（MDP）问题。 方法就是通过动态规划来评估一个给定的策略，通过不断迭代最终得到最优价值函数。 具体的做法有两个：一个是策略迭代，一个是值迭代。

所谓的模型未知，即状态转移概率 \(P_{ss’}^a\) 这些我们是不知道的。 所以我们无法直接利用Bellman方程来求解得到最优策略。

Monte-Carlo Learning

• MC methods learn directly from episodes of experience.
• MC is model-free: no knowledge of MDP transitions/rewards
• MC learns from complete episodes: no bootstrapping
• MC uses the simplest possible idea: value = mean return
• Caveat: can onl apply MC to episodic MDPs
  • All episodes must terminate

我们需要让agent与environment交互，得到一些经历（样本），本质上相当于从概率分布 \(\mathcal{P}_{ss’}^a\)、\(\mathcal{R}\) 中进行采样。 然后通过这些经历来进行策略评估与策略迭代，从而最终得到最优策略。这种做法的理论是从蒙特卡洛方法中来的。

Monte-Carlo Policy Evaluation

The goal is to learn \(v_\pi\) from episodes of experience under policy \(\pi\).

Recall that the return is the total discounted reward:

Recall that the value function is the expected return:

Monte-Carlo policy evaluation uses empirical mean return instead of expected return.

通常情况下某状态的价值等于在多个episode中以该状态算得到的所有收获的平均. 完整的episode不要求起始状态一定是某一个特定的状态，但是要求个体最终进入环境认可的某一个终止状态。 理论上完整的状态序列越多，结果越准确。

• 完整的episode包含的信息有
  • 状态的转移
  • 使用的行为序列
  • 中间状态获得的即时奖励
  • 到达终止状态时获得的即时奖励

First-Visit Monte-Carlo Policy Evaluation

To evaluate state \(s\), the first time-step \(t\) that state \(s\) is visited in an episode. Increment counter \(N(s) \leftarrow N(s) + 1\), increment total return \(S(s) \leftarrow S(s) + G(t)\). Vlue is estimated by mean return \(V(s) = S(s) / N(s)\).

对于每一个episode，仅当该状态\(s\)首次出现的时间\(t\)列入计算

By law of large numbers, \(V(s) \rightarrow v_\pi(s) as N(s) \rightarrow \infty\).

Every-Visit Monte-Carlo Policy Evaluation

To evaluate state \(s\), every time-step \(t\) that state \(s\) is visited in an episode. Increment counter \(N(s) \leftarrow N(s) + 1\), increment total return \(S(s) \leftarrow S(s) + G(t)\). Vlue is estimated by mean return \(V(s) = S(s) / N(s)\).

Again, \(V(s) \rightarrow v_\pi(s) as N(s) \rightarrow \infty\).

Incremental Mean

The mean \(\mu_1, \mu_2, \cdots\) of a sequence \(x_1, x_2, \cdots\) can be computed incrementally,

Incremental Monte-Carlo Updates

Update \(V(s)\) incrementally after episode \(S_1, A_1, R_2, \cdots, S_T\).

For each state \(S_t\) with return \(G_t\):

静态问题就是说我们的MDP是不变的，比如转移矩阵，比如奖励函数

In non-stationary problems, it can be useful to track a running mean, i.e., to forget old episodes:

非静态问题即随着时间的推移，MDP中的某些参数将会发生改变。 此时可以引入参数 \(\alpha\) 来更新状态价值：

这里我们将MC方法变为增量式，便可以使得我们的算法忘掉计数值 \(N(S_t)\)，而换为我们想要的类似于学习速率的参数，该参数的选择关乎算法的收敛性。 在处理非静态问题时，使用这个方法跟踪一个实时更新的平均值是非常有用的，可以扔掉那些已经计算过的episode信息。

MC方法只能用于episodic MDP，也即所有的episode都要终止，否则我们无法计算\(G_t\)。 显然，这种方法计算量会比较大。

Temporal-Difference Learning

• TD methods learn directly from episodes of experience
• TD is model-free: no knowledge of MDP transitions/rewards
• TD learns from incomplete episodes, by bootstrapping
• TD updates a guess towards a guess

先估计某状态在该状态序列完整后可能得到的收获，并在此基础上利用前文所述的累进更新平均值的方法得到该状态的价值，再通过不断的采样来持续更新这个价值。

Bootstrapping

Bootstrapping又叫自助法，是一种通过对样本进行重采样得到的估计总体的方法。

• Bootstrap方法的实质就是一个再抽样过程
  1. 根据观测样本 \(X=[x_1, \cdots, x_n]\) 构造经验分布函数 \(F_n\)
  2. 从 \(F_n\) 中抽取样本 \(X=[x_1, \cdots, x_n*]\)，称其为Bootstrap样本；
  3. 计算相应的Bootstrap统计量, \(R(X, F_n) = \hat{\theta}(F_n) - \hat{\theta}(F_n) \triangleq R_n\)。其中，\(F_n\)是Bootstrap样本的经验分布函数，\(R_n\) 为 \(F_n\) 的Bootstrap统计量
  4. 重复过程 (2) (3) \(N\) 次，即可获得Bootstrap统计量 \(R(X, F_n)\) 的 \(N\) 个可能取值
  5. 用 \(R(X, F_n)\) 的分布去逼近 \(R(X, F_n)\)的分布，可得到参数 \(\theta(F)\) 的 \(N\) 个可能取值，即可统计求出参数 \(\theta\) 的分布及其特征值。

MC and TD

The goal is to learn \(v_\pi\) online from experience under policy \(\pi\).

For incremental every-visit Mone-Carlo, it updates value \(V(S_t)\) toward actual return \(G_t\):

For simple temporal-difference learning algorithm TD(0), it updates value \(V(S_t)\) toward estimated return \(R_{t+1} + \gamma V(S_{t+1})\):

where \(R_{t+1} + \gamma V(S_{t+1})\) is called the TD target; \(\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\) is called the TD error.

显然，MC每次更新都需要等到agent到达终点之后再更新 而对于TD来说，agent每走一步它都可以更新一次，不需要等到到达终点之后才进行更新。

DP vs. TD

DP利用了贝尔曼方程去解强化学习问题 \(V(s) \leftarrow R + \gamma V(S’) \mid s\)

TD 也利用了贝尔曼方程，但是做了以下几点改动：

• 全宽备份变作样本备份：\(s->S\)，并去掉期望符号 \(V(s) \leftarrow R + \gammaV(S’)\)
  1. 智能体跟环境发生交互，采样到哪个当前状态就更新这个状态
  2. 求期望有两种手段，一种是利用概率密度函数加权求和（DP），另一种是利用采样去估计 （TD, MC）
• 增加学习率 \(V(S) \leftarrow V(S) + \alpha (R + \gamma V(S’) - V(S))\)

Bias/Variance Trade-Off

• Return \(G_t = R_{t+1} + \gammaR_{t+2} + \cdots + \gamma^{T-1}R_T\) is unbiased estimate of \(v_\pi(S_t)\)
• True TD target \(R_{t+1} + \gamma v_\pi (S_{t+1}\) is unbiased estimate of \(v_\pi(S_t)\)
• TD target \(R_{t+1}+\gamma V(S_{t+1})\) is biased estimate of \(v_\pi (S_t))
• TD target is much lower variance than the return
  • Return depends on many random actions, transitions, rewards
  • TD target depends on one random action, transition, reward

偏差大（欠拟合）：预测值和样本之间的差 方差大（过拟合）：样本值之间的方差，学出的模型适用性差，意味着样本的置信度较差

Advantages and Disadvantages of MC vs. TD

• TD can learn before knowing the final outcome
  • TD can learn online after every step
  • MC must wait until end of episode before return is known
• TD can learn without the final outcome
  • TD learn from incomplete sequences
  • MC can only learn from complete sequences
  • TD works in continuing (non-terminating) environments
  • MC only works for episodic environment

MC算法只有奖励值作为更新的驱动力 TD算法有奖励值和状态转移作为更新的驱动力

• MC has high variance, zero bias
  • good convergence properties
  • not very sesitive to initial value
  • very simple to understand and use
• TD has low variance, some bias
  • Usually more efficient than MC
  • TD(0) converges to \(v_\pi(s)\)
  • more sensitive to initial value

MC零偏差；高方差；收敛性较好（即使采用函数逼近）；对初始值不敏感；简单、容易理解和使用；随着样本数量的增加，方差逐渐减小，趋近于0。

TD有一些偏差；低方差；表格法下 TD(0) 收敛到 \(v_\pi(s)\) （函数逼近时不一定）；对初始值更敏感（用到了贝尔曼方程）；通常比MC更高效；随着样本数量的增加，偏差逐渐减少，趋近于0。

Batch MC and TD

• MC and TD convergence: \(V(s) \rightarrow v\pi(s)\) as experience \(\rightarrow \infty\)

Certainty Equivalence

• MC converges to solution with minimum mean-squared error
  • best fit to the observed returns

MC算法试图收敛至一个能够最小化状态价值与实际收获的均方差的解决方案

• TD(0) converges to solution of max likelihood Markov model
  • solution to the MDP that best fits the data

TD算法试图收敛至一个根据已有经验构建的最大似然马尔可夫模型的状态价值，也就是说TD算法将首先根据已有经验估计状态间的转移概率

同时估计某一个状态的即时奖励

• TD exploits Markov property
  • Usually more efficient in Markov environments
• MC does not exploit Markov property
  • Usually more effective in non-Markov environment

Unified View

MC学习算法、TD学习算法和DP算法都可以用来计算状态价值 MC和TD是两种在不依赖模型的情况下的常用方法，这其中又以MC学习需要完整的状态序列来更新状态价值，TD学习则不需要完整的状态序列 DP算法则是基于模型的计算状态价值的方法

Bootstrapping and Sampling

• Bootstrapping: update involves an estimate
  • MC does not bootstrap
  • DP bootstraps
  • TD bootstraps
• Sampling: update samples an expectation
  • MC samples
  • DP does not sample
  • TD samples

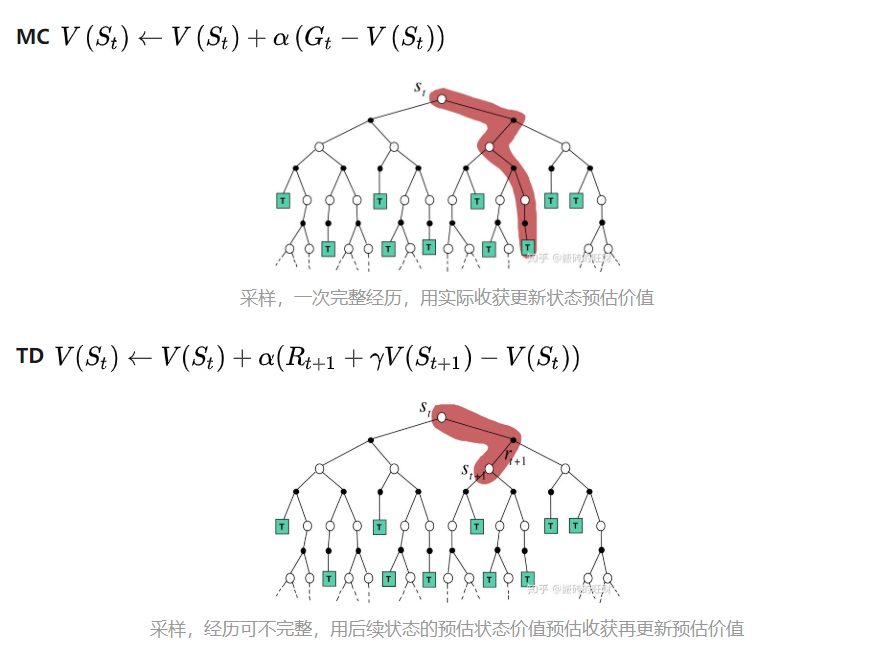
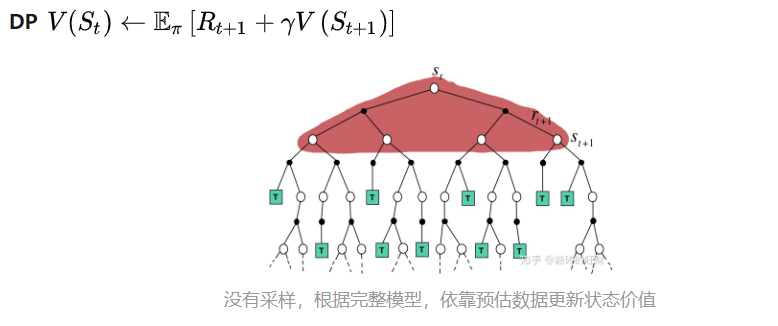
MC学习并不使用引导数据，它使用实际产生的奖励值来计算状态价值 TD和DP则都是用后续状态的预估价值作为引导数据来计算当前状态的价值。

MC和TD不依赖模型，使用的都是个体与环境实际交互产生的采样状态序列来计算状态价值的 而DP则依赖状态转移概率矩阵和奖励函数，全宽度计算状态价值，没有采样之说。

Conclusion

• 当使用单个采样，同时不经历完整的状态序列更新价值的算法是TD学习
• 当使用单个采样，但依赖完整状态序列的算法是MC学习
• 当考虑全宽度采样，但对每一个采样经历只考虑后续一个状态时的算法是DP学习
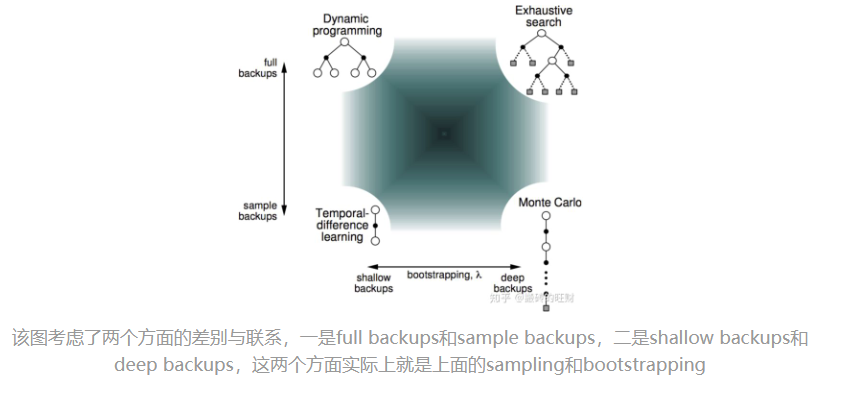
  • DP利用的是整个MDP问题的模型，也就是状态转移概率，虽然它并不实际利用采样经历，但它利用了整个模型的规律，因此也被认为是全宽度（full width） 采样的。
• 如果既考虑所有状态转移的可能性，同时又依赖完整状态序列的，那么这种算法是穷举（exhausive search）法。

TD(λ)

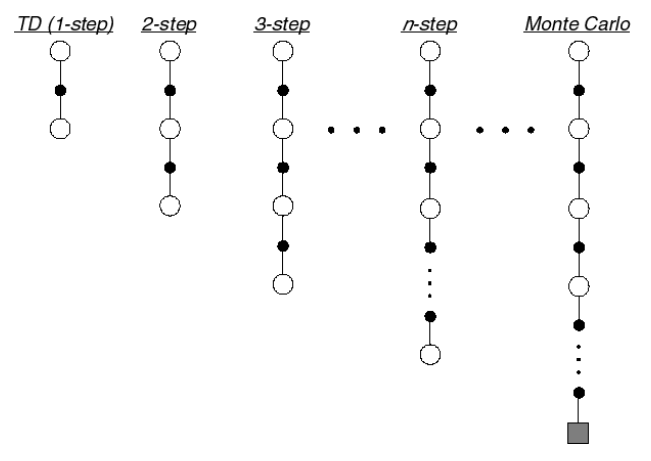
n-Step Return

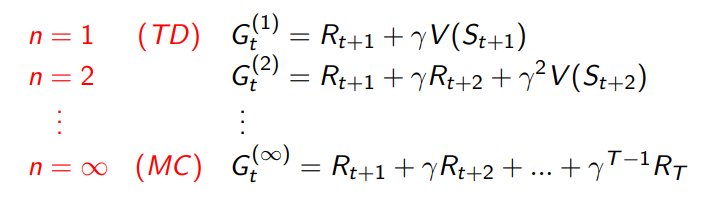
Define the n-step return:

n-step temporal-difference learning:

离线是在经历所有episode后进行状态价值更新 而在线则至多经历一个episode就更新依次状态价值。

Averaging n-Step Returns

We can average n-step returns over different n. For example, average the 2-step and 4-step returns:

To combine information from two different time-steps.

The λ-return \(G_t^\lambda\) combines all n-step returns \(G_t^{(n)}\). Using weight \((1-\lambda)\lambda^{n-1\)

λ=0 退化成 TD(0) ，λ=0 退化成 MC.

Forward-view TD(λ)

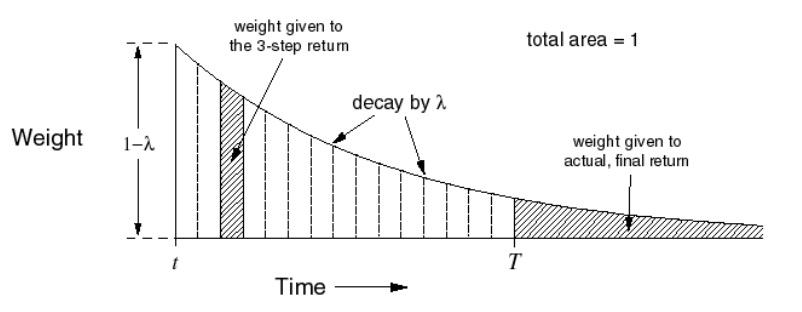
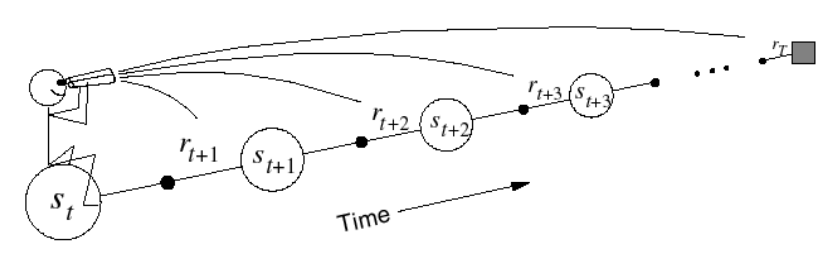
Update value function towards the λ-return. Forward-view looks into the future to compte \(G_t^\lambda\). Like MC, can only be computed from complete episodes.

Backward View TD(λ)

Backward view provides mechanism. Update online, every step, from incomplete sequences.

Eligibility Traces

Frequency heuristic: assign credit to most frequent states.

Recency heuristic: assign credit to most recent states.

Eligibility traces combine both heuristics:

其中 \(1(S_t=s)\) 是一个条件判断表达式，我们可以表示为下面的形式：

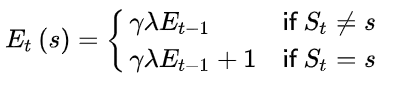
当某一状态连续出现，\(E\) 值会在一定衰减的基础上有一个单位数值的提高，此时将增加该状态对于最终收获贡献的比重，因而在更新该状态价值的时候可以较多地考虑最终收获的影响。同时如果该状态距离最终状态较远，则其对最终收获的贡献越小，在更新该状态时也不需要太多的考虑最终收获。

Keep an eligibility trace for every state \(s\), update value \(V(s)\) for every state \(s\).

每个状态 \(s\) 都保存了一个资格迹。我们可以将资格迹理解为一个权重，状态 \(s\) 被访问的时间离现在越久远，其对于值函数的影响就越小，状态 \(s\) 被访问的次数越少，其对于值函数的影响也越小。

In proportion to TD-error \(\sigma_t\) and eligibility trace \(E_t(s)\):

Relationship Between Forward and Backward TD

When \(\lambda = 0\), only current state is updated. This is exactly equivalent to TD(0) update.

When \(\lambda = 1\), credit is deferred until end of episode. Consider episodic environments with offline updates. Over the course of an episode, total update for TD(1) is the same as total update for MC.

Theorem: The sum of offline updates is identical for forward-view and backward-view TD(λ)

TD(1) is roughly equivalent to every-visit MC. Error is accumulated online, step-by-step. If value function is only updated offline at end of episode, then total update is exactly the same as MC.

• Offline updates
  • Updates are accumulated within episode
  • but applied in batch at the end of episode
• Online updates
  • TD(λ) updates are applied online at each step within episode
  • Forward and backward-view TD(λ) are slightly different
  • NEW: Exact online TD(λ) achieves perfect equivalence
  • By using a slightly different form of eligibility trace

Summary

• 无模型学习
  • 未知环境模型
  • 需要与环境进行交互，有交互成本
  • 样本备份
  • 异步备份
  • 需要充分的探索
  • 两个策略（行为策略和目标策略）
• 动态规划
  • 已知环境模型
  • 不需要直接交互，直接利用环境模型推导
  • 全宽备份
  • 同步和异步
  • 无探索
  • 一个策略

• Previous
  David Silver - Reinforcement Learning Note 3
• Next
  Algorithm for Reinforcement Learning 1