Games GVGAI VGDL

GVGAI Book Chapter 3 - Planning in GVGAI

Posted by Rasin on April 12, 2021

书籍网站

本章原文

本章练习

简介

Planning是指制定行动计划以解决给定的问题。当给定当前状态和玩家要采取的行动时，可以使用环境模型来模拟可能的未来状态，该模型将被称为前向模型（Forward Model）。Monte Carlo Tree Search（MCTS）和Rolling Horizon Evolutionary Algorithms（RHEA）是构建大多数Planning Ai的基础，这两种方法互不相同：第一种方法从可能的游戏动作和状态种构建树，提取统计信息以决定在任何给定状态下下一步该怎么做；第二种方法一开始就定好整个计划，并使用进化计算来组合和修改它们，从而最终获得在游戏中执行的最佳选择。

GVGAI问题可以看作是多目标优化问题：游戏中的计分系统可能具有欺骗性，并且AI不仅需要专注于获得得分（如在传统的街机游戏中一样），而且还需要着眼于解决问题和赢得比赛，甚至还要考虑时间限制。

蒙特卡洛搜索树

该算法通过一次添加单个节点来构建以不对称方式增长的搜索树，并通过使用从节点状态到游戏结束的自玩游戏来估算其游戏理论值。 书中的每个节点都会保存某些统计数据，这些统计数据表明在状态 \(s\) 下选择动作 \(a\) 时获得的奖励实验均值 \(Q(s, a)\)，从给定状态 \(s(N(s, a))\) 以及访问状态 \(s\) 的次数 \(N(s)\)。该算法通过模拟游戏中的动作，在连续的迭代中构建树，并根据这些统计信息做出选择。

MCTS的每个迭代都基于这几个步骤：

  • 树选择
  • 扩展
  • 模拟
  • 后向传播

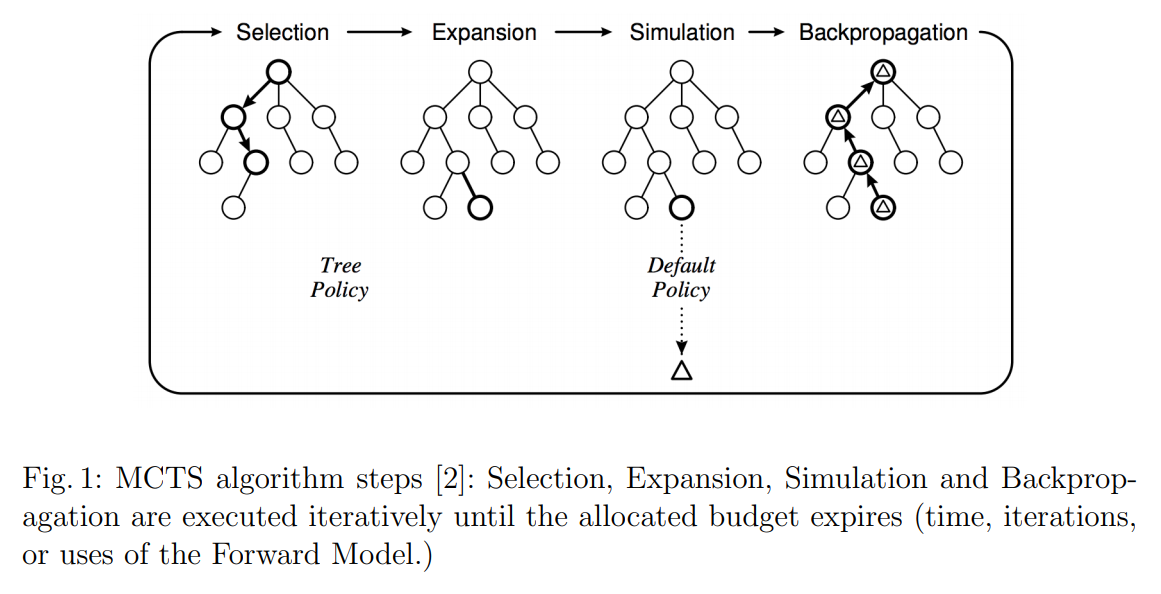
Figure 1

刚开始，树只由根节点组成，存储了当前的游戏状态。在扩展 步骤中，如果游戏还未结束，树从根部开始搜索到一个最大深度。在这一步中，动作可以用 multi-armed bandit策略将其应用到前向模型中。

Multi-armed bandit 策略来源于一个多臂老虎机。当摇动杆时，从一个未知的概率分布返回一个奖励 \(r\)。这个问题的目的是在按一定顺序摇动杆后最大程度减少后悔（或者最大化累计奖励）。这里后悔被定义成一个当选择到一个并非最优的杆时的机会损失。好的政策通过平衡对可用杆的探索与对过去提供更好回报的杆的利用之间的平衡来选择行动。

Upper Confidence Bound (UCB1)：

\[a* = \underset{a\ \in \ A( s)}{\mathrm{argmax}} \ \Bigl\{Q( s,\ a) \ +\ C\sqrt{\frac{\ln N( s)}{N( s,a)}}\Bigr\}\]

该函数的目标是找到一个动作 \(a\)可以使UCB1函数最大化。\(Q(s, a)\)看作是 发掘项，第二项是 探索 项。探索项与给定状态 \(s\)，每个动作 \(a\)被选择的参数\(N(s,a)\)，以及从当前状态中选取动作的数量\(N(s)\)。参数 \(C\)用于平衡发掘与探索。当\(C\) 为0时，UCB1采用贪婪策略每次都选择平均当前收益最高的动作。如果奖励 \(Q(s, a)\)被正则化到 \([0, 1]\) 之间，常用的常数值为 \(\sqrt{2}\)。不同游戏常数值的选择可能不同。

在 树选择 步骤中，直到找到子节点少于动作数量的节点。 此时，在 扩展 步骤加入一个子节点，开启 模拟 步骤。从新节点开始，MCTS执行蒙特卡洛模拟。这时候选择一个随机的动作（均匀随机或有偏随机）一直到游戏结束（或到达一个预定义的深度）。最后，在 反向传播 步骤中，使用状态评估中获得的奖励，为遍历的每个节点更新统计量 \(N(s), N(s, a), Q(s, a)\)。这些步骤会循环执行，直到达到一个结束条件（例如迭代次数或者预计的时间）。

直到所有的迭代完成，MCTS将会推荐agent在游戏中采取的动作。该推荐策略根据存储在根节点中的统计信息来确定动作。可能推荐最近常采用的动作或者得到最高平均收益的策略，也可能直接计算公式得到返回的动作。以下为MCTS算法的伪代码：

pseudocode

MCTS被认为是随时可用的算法，因为它能够在任何时刻提供有效的下一步选择。 这不同于其他算法（例如单人游戏中的A*算法，以及两人游戏中的标准“Min-Max”），这些算法通常仅在完成后才提供给下一次游玩。这使MCTS在实时领域十分合适，在实时域中，决策时间预算受到限制，从而影响了可以执行的迭代次数。

GVGAI也提供了基础版本的MCTS。在实际应用中，\(C\) 选取为 \(\sqrt{2})\)，且rollout深度定为10 。在模拟阶段结束时达到的每个状态都使用该时刻的游戏得分进行评估，并在比赛期间见过的最小和最大得分之间进行归一化。 如果状态为终局，则分配的奖励为较大的正数（如果游戏获胜）或负数（如果游戏输了）。

虽然MCTS在GVGAI平台上的表现很好，但是没有游戏相关的知识支撑算法。Value function 仅基于得分和游戏结束状态，这些概念存在于所有游戏中，因此通常在GVGP方法中使用。

代码示例

以一个简单的游戏为例，该游戏的目的是使每次动作选取数字的累积和接近0.动作的可选范围是 [-2, 2, -3, 3] * 回合数。

首先构建 State 类：

class State():
    NUM_TURNS = 10 #最多10回合
    GOAL = 0 #目标是累计和为 0
    MOVES = [2, -2, 3, -3] # 动作可选范围
    MAX_VALUE = (5.0 * (NUM_TURNS - 1) * NUM_TURNS) / 2 # 最大值为225
    num_moves = len(MOVES) # 动作数量

    # 初始化类
    # 累计和为0，动作为空列表，总回合数由传入参数决定
    def __init__(self, value=0, moves=[], turn=NUM_TURNS):
        self.value = value
        self.moves = moves
        self.turn = turn

    # 下一个状态
    # 通过当前状态得到下一状态
    def next_state(self):
        # 从回合数乘动作的列表中随机选择
        nextmove = random.choice([x * self.turn for x in self.MOVES])
        # 更新下一个状态的成员值
        next = State(self.value + nextmove, self.moves + [nextmove], self.turn - 1)
        # 返回下一个状态
        return next

    # 终结状态
    def terminal(self):
        # 如果剩余回合数为0
        if self.turn == 0:
            # 结束
            return True
        return False

    # 奖励
    def reward(self):
        # 游戏的奖励定义为
        # 用1减去当前值减去目标值的绝对值除以最大值
        # 实际上就是归一化之后距离0越近奖励越多
        r = 1.0 - (abs(self.value - self.GOAL) / self.MAX_VALUE)
        return r

    # 若对象在其生命周期内保持不变，而且能与其他对象相比较，那么这个对象是可哈希的
    # 通过__hash__返回一个int值，用来标记这个对象。
    # 这里是通过操作序列来标记两个状态是否相同
    def __hash__(self):
        return int(hashlib.md5(str(self.moves).encode('utf-8')).hexdigest(), 16)

    # 在调用 `==` 操作符，，实际上是调用 `__eq__`方法
    def __eq__(self, other):
        if hash(self) == hash(other):
            return True
        else False

    # __repr__主要用于调试和开发
    # 用于打印内容
    # repr()更能显示出对象的类型、值等信息，对象描述清晰
    def __repr__(self):
        s = "Value: %d; Moves: %s" % (self.value, self.moves)
        return s

之后定义蒙特卡洛树类：

class Node():
    def __init__(self, state, parent=None):
        self.visits = 1 # 被访问次数默认为1
        self.reward = 0.0 # 奖励为0
        self.state = state # 初始状态
        self.children = [] # 子节点为空列表
        self.parent = parent # 初始父节点

    # 为蒙特卡洛树增加子节点
    def add_child(self, child_state):
        # 直接在子节点列表里面添加一个实例，状态为子节点状态，子节点的父节点是自己
        child=Node(child_state, self)
        self.children.append(child)

    # 更新状态
    def update(self, reward):
        # 更新奖励，且访问数量加1
        self.reward += reward
        self.visits += 1

    # 判断是否完全拓展
    def fully_expanded(self):
        # 如果子节点的数量已经与状态中的动作数量相等了，则已搜索完毕
        if len(self.children) == self.state.num_moves:
            return True
        return False

    # 打印内容
    def __repr__(self):
        s = "Node; children: %d; visits: %d; reward: %f" % (len(self.children), self.visits, self.reward)
        return s

在定义完基本数据结构之后，就要定义策略方法了。首先定义默认策略：

def DEFAULTPOLICY(state):
    # 如果还未搜索结束
    while state.terminal() == False:
        # 则继续搜索 找到下一个状态
        state = state.next_state()
    # 返回奖励值
    return state.reward()

def EXPAND(node):
    # 首先先找出已经搜索过的子节点，保存下来
    tried_children = [c.state for c in node.children]
    # 找到该状态的下一个状态
    new_state = node.state.next_state()
    # 循环验证，若该状态已被尝试
    while new_state in tried_children:
        # 再增加一个新状态，直到没有重复
        new_state = node.state.next_state()
    # 将新状态加入子节点
    node.add_child(new_state)
    # 返回最后一个节点
    return node.children[-1]

def TREEPOLICY(node):
    # 如果有多种选择时且你不想要完全扩展时的一个强制“发掘“的奇技淫巧

    # 在还未完结 时
    while node.state.terminal() == False:
        # 如果子节点数量为0
        if len(node.children) == 0:
            # 扩展
            return EXPAND(node)
        # 随机，二分之一概率
        elif random.uniform(0, 1) < 0.5:
            # 找到最佳子节点
            node = BESTCHILD(node, SCALAR)
        # 否则
        else:
            # 如果还未完全扩展
            if node.fully_expanded() == False:
                # 扩展
                return EXPAND(node)
            # 否则返回最佳子节点
            else:
                node = BESTCHILD(node, SCALAR)
    return node

def BESTCHILD(node, scalar):
    # 最高分初始为0
    bestscore = 0.0
    # 最佳子节点列表为空
    bestchildren = []
    # 遍历所有的子节点
    for c in node.children:
        # 根据公式计算
        # 发掘项
        exploit = c.reward / c.visits
        # 探索项
        explore = math.sqrt(2.0 * math.log(node.visits) / float(c.visits))
        # UCB1总分为两者之和
        score = exploit + scalar * explore

        # 找到最高分
        if score == bestscore:
            bestchildren.append(c)
        if score > bestscore:
            bestchildren = [c]
            bestscore = score

    # 如果最佳子节点数量为0，则报错
    if len(bestchildren) == 0:
        logger.warn("OOPs: no best child found, probably fatal")
    # 随即返回一个最佳子节点
    return random.choice(bestchildren)

# 反向传播
def BACKUP(node,reward):
	while node!=None:
		node.visits+=1
		node.reward+=reward
		node=node.parent
	return

总搜索函数为：

# 输入耗费预算和根节点
def UCTSEARCH(budget, root):
    # 在预算范围内循环
    for iter in range(int(budget)):
        # 每10000次打印一次
        if iter%10000 == 9999:
            logger.info("simulation: %d" %iter)
            logger.info(root)

            # 通过TreePolicy找到最佳子节点
            front = TREEPOLICY(root)
            # 得到奖励
            reward = DEFAULTPOLICY(front.state)
            # 反向传播
            BACKUP(front, reward)
    # 返回最佳策略
    return BESTCHILD(root, 0)

那么一个完整的执行过程写在 main 函数中：

if __name__ == '__main__':
    parser = argparse.ArgumentParser(description='MCTS research code')
    # 模拟预算参数
    parser.add_argument('--num_sims', action="store", required=True, type=int)
    # `levels` 是使用MCTS挑选最佳子节点的次数 
    parser.add_argument('--levels', action="store", required=True, type=int, choices=range(State.NUM_TURNS))
    args = parser.parse_args()

    # 定义空树
    current_node = Node(State())
    for l in range(args.levels):
        current_node = UCTSEARCH(args.num_sims / (l + 1), current_node)
        print("level %d" % l)
        print("Num Children: %d" % len(current_node.children))
        for i, c in enumerate(current_node.children):
            print(i, c)
        print("Best Child: %s" % current_node.state)

        print("--------------------------------")

若 num_sims 为 100000，深度 levels 为 9，一次模拟结果为：

level 0
Num Children: 2
0 Node; children: 0; visits: 2; reward: 0.928889
1 Node; children: 0; visits: 2; reward: 0.920000
Best Child: Value: -30; Moves: [-30]
--------------------------------
level 1
Num Children: 1
0 Node; children: 0; visits: 2; reward: 0.911111
Best Child: Value: -3; Moves: [-30, 27]
--------------------------------
level 2
Num Children: 1
0 Node; children: 0; visits: 2; reward: 0.813333
Best Child: Value: -27; Moves: [-30, 27, -24]
--------------------------------
level 3
Num Children: 1
0 Node; children: 0; visits: 2; reward: 0.826667
Best Child: Value: -48; Moves: [-30, 27, -24, -21]
--------------------------------
level 4
Num Children: 2
0 Node; children: 0; visits: 2; reward: 0.848889
1 Node; children: 0; visits: 2; reward: 0.764444
Best Child: Value: -30; Moves: [-30, 27, -24, -21, 18]
--------------------------------
level 5
Num Children: 0
Best Child: Value: -20; Moves: [-30, 27, -24, -21, 18, 10]
--------------------------------
level 6
Num Children: 0
Best Child: Value: -12; Moves: [-30, 27, -24, -21, 18, 10, 8]
--------------------------------
level 7
Num Children: 0
Best Child: Value: -6; Moves: [-30, 27, -24, -21, 18, 10, 8, 6]
--------------------------------
level 8
Num Children: 0
Best Child: Value: -12; Moves: [-30, 27, -24, -21, 18, 10, 8, 6, -6]
--------------------------------

基于知识的快速进化MCTS

MCTS中的快速进化

KB Fast-Evo MCTS 使用进化算法从环境中来学习rollout polic。该算法使用进化方法来调整一系列权重 \(w\)对蒙特卡洛模拟进行偏移。这些权重可用于结合针对当前游戏状态提取的一组固定功能来选择每个步骤的动作。

每一次 rollout 均使用最后到达的状态值作为适应性对单组权重进行评价。使用到的进化权重的算法为 (1+1)进化策略。该策略的伪代码如下：

Algorithm 2

第三行的调用检索了下一个个体来评估 (w)， a 和适应值在第八行给定。权重 w的向量用于便宜 rollout（第六行）。对于每个在 rollout 中找到的状态，首先 N 个数量的特征被提取（从状态空间\(S\)到特征空间\(F\)）。给定可行的动作 A，特征的权重和值制定了每个动作的相对强度 \((a_i)\)，如下列公式所示：

\[a_i = \sum_{j=1}^N w_{ij} \times f_i\]

这些动作都是经过特征加权过的动作，权重都存在矩阵 \(W\) 中，每一项 \(w_{ij}\) 代表对动作\(i\)经过特征 \(j\) 的权重。最后用一个softmax函数来选择蒙特卡罗模拟：

\[P(a_i) = \frac{e^{-a_i}}{\sum^{A}_{j=1} e^{-a_j}}\]

实际上，这些特征取决于游戏中特定精灵贴图的存在和消失，N特征的数量不仅每个游戏中不同，可能每个步骤中都不同。因此，该算法对于每个步骤中特征数量的加权需要更加灵活。

学习领域知识

定义 KB Fast-Evo MCTS 的下一步便是增加一个可以提供更强力的你和函数系统来使得个体进化。你和实在rollout结束的时候计算的，目标是顶一个一个状态估计函数，这个函数的知识是在玩游戏的时候 动态学习的。

为了构建这个函数，知识库可以被分解为两个部分：好奇心 + 经验。好奇心指的是去发现与其他精灵贴图碰撞时产生的效果，经验 权衡那些能够提供分数增长的事件。事件记录可能是主角再碰到其他对象或者产生一些其他精灵贴图后提取的（如NPC，资源，非静态对象和传送门等）。每个 知识项 包含了以下统计数据：

  • \(Z_i\): 事件 \(i\) 发生的概率
  • \(\bar{x_i}\): 分数的变化的平均值，即事件发生前后游戏分数之间的变化。多个事件在同一个游戏时间片中发生，可能无法确定哪个事件出发了得分变化。因此，事件发生概率 \(Z_i\)越大，分数变化平均值 \(\bar{x_i}\)就越准确。

这两个值在蒙特卡洛模拟的每次前向模型调用时更新。当达到rollout结束时的状态，下面的值将被计算：

  • 分数变化 \(\triangle R\): 初始状态和结束状态之间的游戏分数变化
  • 好奇心：知识改变 \(\triangle Z = \sum_{i=1}^N \triangle (K_i)\)用于测量知识库中对于每个知识项\(i\)，所有 \(Z_i\) 的变化。\(\triangle (K_i)\) 由下列公式计算，其中 \(Z_{i0}\)是 \(Z_i\) 的初始值，\(Z_{iF}\) 是\(Z_i\)的最终值。当 rollouts 产生更多事件时，\(\triangle Z\) 会更高。如果某个事件非常稀有，则会提供较高的 \(\triangle Z\) 值，有利于模拟中的知识收集。：
\[\triangle (K_i) = \begin{cases} Z_{iF} & Z_{i0} =0\\ \frac{Z_{iF}}{Z_{i0}} -1 & otherwise \end{cases}\]
  • 经验： \(\triangle D = \sum_{i=1}^{N} \triangle (D_i)\) 经验是一种从 rollout 开始到结束到每个类型为 \(i\) 精灵贴图的距离变化的度量。以下函数定义了 \(\triangle (D_i) \)，其中 \(D_{i0}\) 是 rollout 开始时到最接近类型 \(i\) 精灵贴图的距离，\(D_{if}\) 是 rollout 结束时的距离。如果玩家在 rollout 期间与那些已知精灵贴图减少了 \(\bar{x_i}\) 的距离而不是那些未知贴图的距离，那么 \(\triangle D\) 就会变得更高。
\[\triangle (D_i) = \begin{cases} 1-\frac{D_{iF}}{D_{i0}} & Z_{i0} =0\ or\ \left( D_{i0} \ >0\ and\ \overline{x_{i}} >0\right)\\ 0 & otherwise \end{cases}\]

下列函数表示了游戏状态的最终值以及对于评估个体的拟合。这个值称为 \(\delta R \)，除非 \(\triangle R =0 \)。当其为0时，rollout 中的所有的动作都无法改变游戏分数。下列函数以 \(\alpha = 0.66\) 和 \(\beta = 0.33\) 为参数定义了一个线性函数：

\[Reward = \begin{cases} \triangle R & \triangle R\neq 0\\ \alpha \triangleserifs Z\ +\ \beta \triangle D & otherwise \end{cases}\]

因此，新的值函数将优先权分配给产生得分增加的动作。但如果没有分数增加的话，则把优先权分配给提供给知识库更多信息或者使玩家更接近提供分数精灵贴图的动作。

CATALOG
    FEATURED TAGS
    Computer Vision Colorization Deep Learning Papers Technical Writing Computer Graphics Tutorials Mathematics Graph Neural Network Biomedical Natural Language Processing Graph Theory Neural Network Reinforcement Learning Markov Decision Process Paper Reading Games GVGAI VGDL MCTS Clustering Unsupervised Machine Learning Social Science