蒙特卡洛树搜索
蒙特卡洛树搜索基于两个重要的基本概念:使用随机模拟的方法可能能够模拟动作的真实值;这些值可能可以用于调整最佳优先策略。该算法逐步构建一个局部博弈树,以之前探索的结果作为引导。这棵树用于估计动作的值,逐渐使这些值在构建过程中变得更加准确。
算法
基本算法包括迭代构建搜索树,直到到达一些预定义的 computational budge(一般为时间、内存或迭代约束)为止,这时停止搜索并返回性能最佳的根操作。搜索树中的每个节点表示域的状态,指向子节点的定向链接表示导致后续状态的动作。
在每个搜索迭代中执行四个步骤:
- 选择:起始于根节点,子节点选择策略将递归应用到树中,直到到达最需要的可扩展结点为止。如果节点表示非终止状态并且具有未访问节点,则该节点是可扩展的。
- 扩展:将一个或多个子节点根据当前可用的动作加入当前节点来扩展树。
- 模拟:根据缺省策略从新节点运行模拟以产生结果。
- 反向传播:将模拟的结果进行“备份”(即,反向传播)以更新其统计信息。
根据以上过程可以分为两个不同的策略:
- 树策略:从搜索树中已经包含的节点中选择或创建叶节点(选择和扩展)
- 缺省策略:从给定的非终结状态执行动作来产生值估计(模拟)
反向传播过程并不会使用策略本身,但更新节点统计信息时将会影响未来的树策略。

在伪代码中,\(v_0\) 是根节点,也代表着初始状态 \(s_0\) ,\(v_l\)是根据树策略阶段最后遇到的节点,对应着状态 \(s_l\), \(\triangle\) 是通过运行状态 \(s_l\) 中的缺省策略而获得的终止状态的奖励。整体搜索结果 \(a(BestChild(v_0))\) 是导致根节点 \(v_0\)找到最佳子节点的动作 \(a\),其中最佳的定义由实现决定。
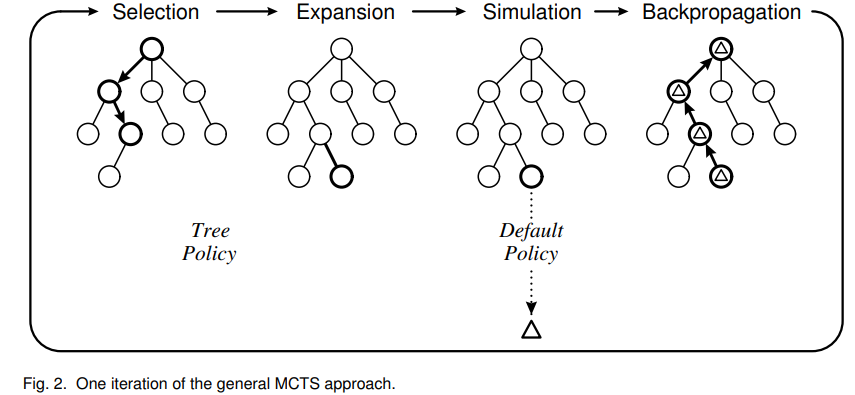
图二显示了一次MCTS算法的迭代。从根节点 \(t_0\) 开始,根据某些效用函数递归选择子节点,直到到达描述终止状态或未完全扩展的节点 \(t_n\)。从该状态 \(s\) 选择一个未访问的动作 \(a\),将新的子节点 \(t_l\) 添加到树种,该子节点描述了从状态\(s\)将动作\(a\)应用到状态 \(s’\)。这样就完成了此次迭代的树策略部分。
之后,模拟从新扩展的叶节点 \(t_l\)产生新的奖励值 \(\triangle\),之后将这一系列的节点后向传播为此迭代选择的节点序列,以更新节点统计信息。每个节点的访问次数都会增加,并且其平均奖励或\(Q\)值会根据\(\triangle\)进行更新。奖励值 \(\triangle\)可能是离散的或连续的,或者也可能是在多agent领域的一个向量形式。
一旦搜索被终端或达到预计的computational budge,搜索就会停止,并且根节点 \(t_0\)的动作 \(a\)将通过某种机制进行选择。
选择获胜行为的四个标准:
Max child: 选择奖励最高的子节点Robust child: 选择最经常访问的子节点Max-Robust child: 选择有最高奖励和最经常访问的子节点。如果不存在,则继续搜索直到找到一个可接受的结果。Secure child: 选择最大置信度下限的子节点
发展

树的上置信界
UCT 算法
MCTS的目标是从当前状态去近似可以被选用动作的博弈论值。如何构建树取决于如何选择节点。MCTS的成功也主要归功于树策略。UCB1将子节点的选择视为多臂赌博机,子节点的值是通过蒙特卡洛模拟近似的预期奖励,因此这些奖励对应于具有位置分布的随机变量。
UCB1具有一些很不错的性质:它非常的简单有效,并且保证在一定的范围内始终保持最大的遗憾增长率。因此,此算法是解决MCTS中的 探索-发掘困境 的一个强力候选者:每当要在现有树种选择一个节点(动作)时,就可以将这个选择建模成一个独立的多臂赌博机问题。选择一个子节点 \(j\) 以最大化:
其中,\(n\)时当前(父)节点被访问的次数,\(n_j\)是子节点 \(j\)被访问的次数,\(C_p > 0\) 是个常数。如果多个子节点有相同的最大值,则随机选择。\(\bar{X}_j\)取值在 [0, 1] 之间。若\(n_j=0\),则 UCT值将会无穷大,因此之前未访问的节点都将这个值设为最大值来保证所有的子节点都能至少被考虑到一次。这导致了一种强大的迭代本地搜索形式。
在 UCB 中维持了一种探索(第二项)和发掘(第一项)的平衡。随着节点的访问,探索的分母逐渐增加,导致其比重逐渐下降。另一方面,如果访问了父节点的另一个子节点,则分子增加,因此为访问的兄弟姐妹的探索值增加。探索项可确保每个孩子的选择概率都不为0,这对于游玩的随机性至关重要。这意味算法附有了固有的 重启 属性,因为即使是低奖励的子节点也可以保证最终被选择(如果由足够的时间),因此可以探索不同的游戏路线。
在公式中的常数 \(C_p\)可以被调整得更高或更低,于探索的水平相关。默认值被设置为 \(C_p = \frac{1}{\sqrt{2}}\) 是为了满足Hoeffding不等式,且奖励落于[0, 1]之间。若奖励落在这个区间外,我们可能就需要另一个 \(C_p\)。
算法的剩余部分就如同本章3.1部分叙述的那样:如果通过UCB下降选择的节点具有尚未成树的子节点,则随机选择其中之一并将其添加到树中。之后使用缺省策略,直到达到终止状态为止。最简单的一个例子是这个缺省策略服从均匀分布。终止状态 \(s_T\)的值 \(\triangle\) 之后反向传播到这个迭代中访问的所有节点中,从最新加的节点到根节点。
每个节点都保存两个值,被访问的次数 \(N(v)\) 和经过该状态是的游玩总奖励 \(Q(v)\)(因此 \(Q(v)/N(v)\)是节点的博弈论值的近似)。每次一个节点是从根部开始的游玩迭代的一部分,那么值就更新。一旦到达了computational budge,或者算法找到最佳玩法并终结时,该最佳玩法便是拥有最高访问量的根的子节点。
算法2显示了UCT算法的伪代码。这份代码消除了现有文献中常见的双人玩家,零和及回合顺序等限制条件。

对于每个节点 \(v\) 就有四条数据与其关联:相关的状态 \(s(v)\),将要执行的动作 \(a(v)\),总模拟奖励 \(Q(v)\)(一个实值向量),以及访问数量 \(N(v)\)。与在每个节点上存储 \(s(v)\) 相比,在书策略下降树时重新计算它通常会在内存使用方面更加有效。\(\triangle (v, p)\)项表示了在当前玩家 \(p\)的 \(v\)节点上与当前关联的奖励向量的分量。
在这里,搜索的返回结果值是 \(a(BestChild(v_0, 0))\),也就是将玩家引领到最高奖励的动作 \(a\),在最后根节点 \(v_0\)的调用上探索参数 \(c\)被设为0。该算法可以返回访问量最大的子节点的动作。
算法3显示了另外一种在双人零和轮流动作游戏中更有效率的备份方法。这类似于 minimax 搜索的 negamax 变体,其中在树的每个级别取反标量奖励值以获得其他玩家的奖励。注意, \(\triangle\) 在算法2中被当作每个agent的奖励向量,而在算法3中它是单个标量值,表示agent运行的搜索。同样的,节点奖励值 \(Q(v)\) 可以被当作是每个玩家 \(Q(v, p)\) 的一个向量,如果需要的话。
收敛到 Minimax
在不稳定的奖励分配的情况下,UCB1 的遗憾边界仍然成立,通过经验证明了MCTS与UCT在各种领域的运用。Kocsis 和 Szepesvari表明,随着模拟游玩数量增长到无穷大,树根故障概率(即选择到次优动作的概率)以多项式速率收敛到零。该证据表明,给定足够的时间(和内存),UCT 允许 MCTS收敛到 Minimax树,因此是最优的。
特性
本节介绍了一些MCTS成为流行算法的特性。
A 启发式
MCTS最重要的好处之一就是不需要特定领域的知识,这使其很容易适用于可以使用树进行建模的任何领域。尽管在博弈论上,全深度的Minimax 是最佳选择,但深度限制 minimax游戏质量在很大程度上取决用于评估叶节点的启发式算法。像在国际象棋这样的游戏中,经过数十年的研究,可靠的启发式方法已经出现,minimax的表现非常出色。但在围棋中,分支因子要大几个数量级,而有用的试探法则很难制定,因此 minimax的性能会大大降低。
尽管可以在没有特定领域知识的情况下应用MCTS,但通常可以使用特定知识来显著提高性能。现在,所有基于MCTS的性能最好的围棋程序都是用基于特定游戏的知识。只要能够以有利的方式偏向移动选择,这种知识就不必是完整的。
使用领域特定知识来偏向移动选择时,需要权衡取舍:统一随机动作选择的优点之一是速度,它允许在给定的时间内执行许多模拟。特定领域的知识通常会极大地减少可能的模拟数量,但也可能会减少模拟结果的差异。关于性能与通用性以及速度之间的权衡问题也需要进一步讨论。
即时性
MCTS对于每个游戏的结果都能即时进行反向传播以确保算法每次迭代后所有值始终是最新的。这允许算法在任何时候从根返回一个动作; 允许算法运行更多次迭代通常可以改善结果。
可以使用迭代加深来近似minimax的任何时间版本。 但是,随着每次迭代将整个层添加到树中,进度的粒度要粗糙得多。
非对称性
树的选择允许算法偏爱更多有希望的节点(不允许其他节点的选择概率收敛到零),从而导致树随时间推移不对称。 换句话说,部分树的构建偏向更有希望的区域,因此也变得更重要。
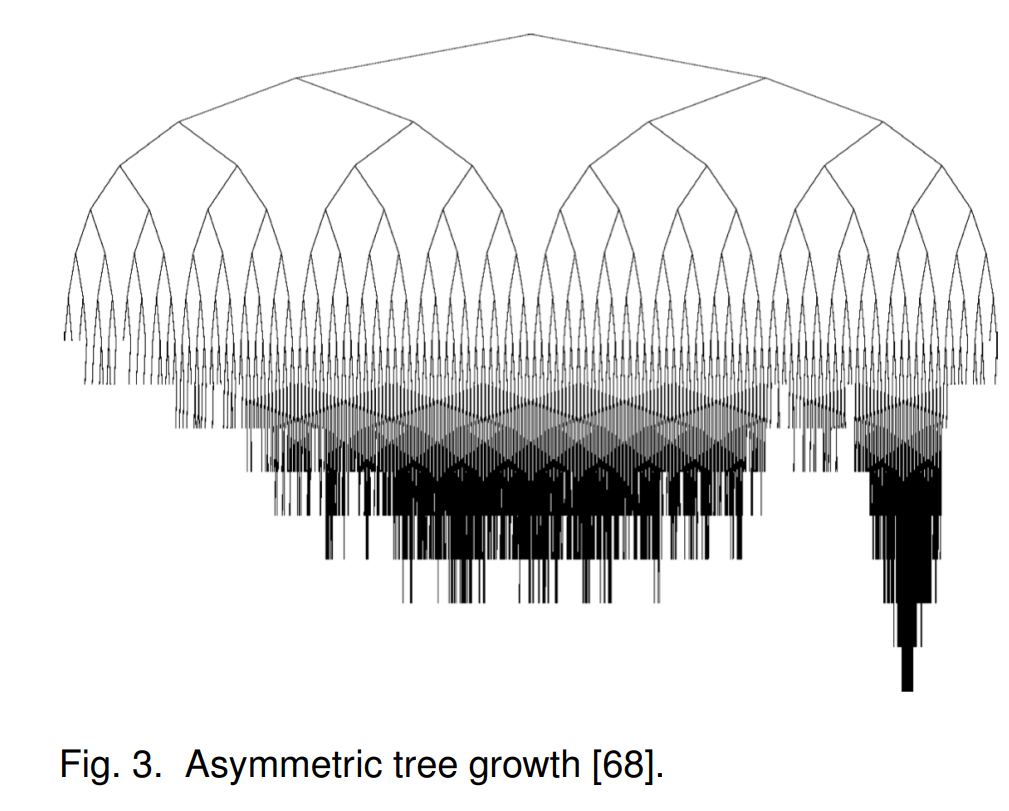
图3显示了使用MCTS的BAST变体生成的不对称树。
与其他算法比较
当我们遇到问题时,可能很难在 minimax 和MCTS之间进行选择。如果有稀疏的大小并不平凡,且不存在可靠的启发式方法,则 minimax 不适用,MCTS是更好的选择。反之,如果特定领域的知识很容易获得,则两种算法都可能是可行的方法。
国际象棋这样的游戏MCTS方法不如围棋那样成功。他们考虑了 UCT 明显优于 minimax 的一类合成空间。特别是该模型会有生成有界树,其中每个状态恰好有一个最佳动作。次优选择会受到固定的附加成本的惩罚。 树的系统构造确保了真正的最小最大值是已知的。 在此领域中,UCT明显胜过minimax,并且性能差距随着树的深度而增加。
术语
文献中以各种方式使用了MCTS和UCT术语,有时不一致,有可能导致所涉及算法的细节混乱。 在本综述的其余部分中,我们遵循以下术语:
- Flat Monte Carlo: 一种基本的蒙特卡洛方法,具有均匀的动作选择并且没有树生长。
- Flat UCB: 一种基于赌博机的动作选择方法的蒙特卡罗方法,没有树生长。
- MCTS: 构建树以实时更新其策略的蒙特卡洛方法 。
- UCT: 具有任何UCB树选择策略的MCTS。
- Plain UCT: MCTS with UCB1。