简介
集中分布的数据集将它们作为同一个数据集进行分析,可以使我们获得新颖的见解,并获得对比单个分布的数据集进行单独分析更高的预测性能。但是由于数据量太大或隐私问题,通常很难集中原始数据集。
例如,医疗数据分析问题中,由于数据样本的不足和不平衡,每个医疗机构中的数据集可能不足以生成高质量的预测结果。然而,由于隐私问题,很难将原始医疗数据样本与其他机构的数据集中在一起。是否可以通过适当的映射将原始数据转换到另一(例如低维)空间。由于中间表示的每个特征都没有现实解释,因此映射的数据(中间表示)可以相当容易地集中化。
与目前现存的方法不同的是,本文提出了一种用于分散数据集的数据聚合分析框架,该框架仅集中单独构建的中间表示。本框架假定每个机构适用不同的映射函数来构建中间表示。本框架没有集中化映射函数,以避免通过使用映射函数的(近似)逆来从原始数据样本的中间表示中得到原始数据样本的风险。该数据聚合分析框架也没有使用隐私保护计算,而使用公共数据和随机模拟的可共享数据来替代。框架通过将各个中间表示映射到称为聚合表示的可合并形式来实现数据协作分析。
本文还针对隐私保护问题提出了一种实用的算法和一种实用的操作策略。通过在人工和现实世界数据集上的数值实验评估了该方法的识别性能,并与集中式分析和单独分析进行了比较。
数据聚合分析框架
本文提出的方法可以被看为是分散数据集的降维方法。分散的原始数据及通过中间表示形式转换为聚合表示形式。因此,在构造了聚合表示之后,我们可以使用任何机器学习算法,包括无监督学习,监督学习和半监督学习。
将设我们有 \(d\)个数据集。\(m, n_i\) 分别是第\(i\)个数据集的特征数量及训练数据样本,\(n\)是训练数据样本的总数,即:
\[n = \sum^d_{i=1} n_i\]另外,令
\[{X}_i = [{x}_{i1}, {x}_{i2}, \cdots, {x}_{in_i}] \in \mathbb{R}^{m\times n_i}\]为第\(i\)个训练数据集。对监督学习来说,我们额外令
\[{L}_i = [{l}_{i1}, {l}_{i2}, \cdots, {l}_{in_i}] \in \mathbb{R}^{l \times n_i}\]为训练数据的正确标签。另外,\(s_i\)为第\(i\)个数据集的测试数据及数量,即:
\[s = \sum_{i=1}^d s_i\]第\(i\)个数据集的测试数据集可以表示为
\[{Y}_i = [{y}_{i1}, {y}_{i2}, \cdots, {y}_{is_i}] \in \mathbb{R}^{m\times s_i}\]我们不将原始数据集中化。我们将从\({X}_i\)单独构建的中间表示集中化。我们也不将映射函数集中化,来降低近似出原始数据的风险。
基本概念与框架
我们将中键表示集中化而不是将原始数据 \({X}_i\)集中化:
\[\tilde{X}_i = [\tilde{x}_{i1}, \tilde{x}_{i2}, \cdots, \tilde{x}_{in_i}] = f_i(X_i) \in \mathbb{R}^{l_i \times n_i}\]其中,\(f_i\)是线性或非线性的逐列映射函数。由于每个映射函数\(f_i\)都是由\(X_i\)单独构建的,因此 \(f_i\)和它的维度 \(l_i\)都取决于 \(i\)。
映射函数可以分为几类,例如无监督降维中的 PCA, LPP;以及有监督降维中的 FDA, LFDA;半监督的 SELF ,LADA;以及基于复杂矩的有监督特征映射 CMSE。另一方面也可以考虑构建深度神经网络。本框架只在通过实现聚合分析来避免集中化分析的困难,同时原始数据集 \(X_i\)和映射函数 \(f_i\)仍分布在每个数据集之中。
由于映射函数 \(f_i\) 由数据集 \(i\)决定,甚至当每个数据集都有相同的数据样本 \(x\),数据的中间表示都会不同,也就是:
\[f_i (x) \neq f_j(x)\]另外,原始数据样本 \(x\) 和 \(y\) 之间的关系通常不会在不同的数据及之间保留,也就是:
\[D(f_i(x), f_j(y)) \napprox D(x, y)\]其中,\(D(\cdot, \cdot)\)表示数据样本之间的关系,例如距离和相似度。因此,不能将数据集的中间表示分析为一个数据集,即使他们的维度是相同的, \(l_i = l_j\)。
为了克服这一困难,作者再次将各个中间表示形式转换为可合并表示形式,如下所示:
\[\hat{X}_i = [\hat{x}_{i1}, \hat{x}_{i2}, \cdot, \hat{x}_{in_i}] = g_i(\tilde{X}_i) \in \mathbb{R}^{l\times n_i}\]其中,\(g_i\) 是逐列映射函数:
\[g_i(f_i(x)) \approx g_j(f_j(x))\] \[D(g_i(f_i(x)), g_j(f_j(y))) \approx D(x, y) (i\neq j)\]保留了原始数据集的关系,我们可以分析获取的数据 \(\hat{X}_i\)就如同单个数据集一样:
\[\hat{X} = [\hat{X}_1, \hat{X}_2, \cdots, \hat{X}_d] \in \mathbb{R}^{l\times n}\]由于用于中间表示的映射函数 \(f_i\) 没有被集中化,函数 \(g_i\)也不能够单独从集中化的中间表示\(\tilde{X}_i\)中构建出来。为了构造映射函数 \(g_i\),我们介绍了称为锚定数据集的可共享数据,该数据集由随机构成的公共数据或虚拟数据组成:
\[X^{anc} = [x^{anc}_1, x^{anc}_2, \cdots, x^{anc}_r] \in \mathbb{R}^{m\times r}\]这里 \(r \geq l_i\)。将每个映射函数 \(f_i\) 映射到锚定数据,我们就拥有了锚定数据的第\(i\)个中间表示:
\[\tilde{X}^{anc}_i = [\tilde{x}^{anc}_{i1}, \tilde{x}^{anc}_{i2}, \cdots, \tilde{x}^{anc}_{ir}] = f_i(X^{anc}) \in \mathbb{R}^{l_i\times r}\]之后,我们将 \(\tilde{X}^{anc}_{i}\)集中化并构建\(g_i\):
\[\hat{X}^{anc}_i = [\hat{x}^{anc}_{i1}, \hat{x}^{anc}_{i2}, \cdots, \hat{x}^{anc}_{ir}] = f_i(\tilde{X}^{anc}) \in \mathbb{R}^{l\times r}\]该函数满足:
\[\hat{X}^{anc}_i = \approx \hat{X}^{anc}_j, D(\hat{x}^{anc}_{ik}, \hat{x}^{anc}_{jl}) \approx D(x^{anc}_k, x^{anc}_l) \ (i \neq j)\]该数据聚合分析框架中的基本过程如下:
- 中间表示构造:每个数据集分别构造器中间表示并将它们集中。
- 聚合表示构造:根据集中的中间表示,来构造聚合表示。
- 聚合分析:从单个原始数据集获得的聚合形式将作为一个完整数据集进行分析。
实用算法
本框架的基本组成部分设计实用锚点数据构建聚合表示(阶段二)。可以使用以下两步骤来构造映射函数 \(g_i\):
目标设定
我们将锚定数据的聚合数据表示\(\hat{X}^{anc}_i\)的目标设定为 \(Z=[z_1, z_2, \cdots, z_3] \in \mathbb{R}^{l \times r}\),使其满足:
\[Z \approx \hat{X}^{anc}_i\]或
\[D(z_k, z_l) \approx D(x^{anc}_k, x^{anc}_l)\]映射函数构建
我们需要构建映射函数 \(g_i\)使之符合:
\[Z \approx g_i(\tilde{X}^{anc}_i)\]虽然步骤一和二有多种计算方法,但本文假设 \(g_i\)是一种线性映射。步骤一仅考虑的 \(Z \approx \hat{X}^{anc}_i\),这里提出一个实用算法:
由于映射函数 \(g_i\)是线性映射,构造矩阵 \(G_i \in \mathbb{R}^{l \times l_i} \)我们有:
\[\hat{X}_i = g_i(\tilde{X}_i) = G_i \tilde{X}_i\] \[\hat{X}^{anc}_i = g_i(\tilde{X}^{anc}_i) = G_i \tilde{X}^{anc}_i\]为了满足 \(Z \approx \hat{X}^{anc}_i\) 的条件,我们提出了一下的最小化问题:
\[\underset{G_{1}^{'} ,G_{2}^{'} ,\cdots ,G_{d}^{'} ;Z}{\min} \ \sum _{i=1}^{d} \| Z-G_{i}^{'}\tilde{X}_{i}^{anc} \| _{F}^{2}\]如果直接解决的话相当困难,因此,我们考虑解决如下的最小扰动问题:
\[\underset{E_{i} ,G_{i}^{'} ,Z}{\min}\sum _{i=1}^{d} \| E_{i} \| _{F}^{2} \ s.t.\ G_{i}^{'}\left(\tilde{X}_{i}^{anc} +E_{i}\right) =Z\]当\(d=2\)时,这个最小扰动问题被称为总最小二乘问题(total least squares problem),且可以使用奇异值分解(SVD)来解决。同样的,当 \(d>2\)的情况下也可以使用 SVD来解决这个问题,令:
为结合 \(\tilde{X}^{anc}_{i}\)的SVD,其中:
且 \(\Sigma_1\)有大量的奇异值。我们有:
\[Z = CU^T_1\]其中,\(C \in \mathbb{R}^{l\times l}\) 是一个非奇异矩阵。
接下来,设定 \(Z = U^T_1\),我们使用 \(Z \approx g_i(\tilde{X}^{anc}_i)\) 来计算\(G_i\)。矩阵 \(G_i\)可以用求解以下的线性最小二程问题来计算得到:
\[G_i = \arg \underset{G}{\min} \| Z - G\tilde{X}^{anc}_i \|^2_F = U^T_1 (\tilde{X}^{anc}_i)^ \dagger\]其中,\((\tilde{X}^{anc}_i)^ \dagger\) 代表了矩阵 \(\tilde{X}^{anc}_i)\) 的Moore-Penrose伪逆。

Algorithm 1总结了在监督学习下提出的算法。
这个方法的主要计算成本之一是对于SVD,其取决于锚点数据数量 \(r\)和中间表示的维度 \(l_i\)。我们可以使用包括 随机SVD在内的一些近似算法来减少计算成本。另一方面,锚点数据 \(X^{anc}\) 也严重影响了所提出方法的性能。一种简单的办法是将 \(X^{anc}\)设为一个随机矩阵。如果锚点数据与原数据具有相同的分布,则可以提高性能。我们打算在将来研究新技术以构建合适的锚点数据。
有关隐私问题的实践操作策略
我们给予提出的监督学习框架,考虑了有关隐私问题的实践操作策略。本文使用术语“隐私”是指他人无法获得相应数据的每个条目。本文不考虑数据集统计信息的隐私问题。
基于这个定义,我们可以断言,对于每个数据集的原始数据 \(X_i\),只要满足一下几个操作策略,隐私就得以保护:
- 两个角色:分别拥有训练和测试数据集的用户以及集中化中间表示并对其进行分析的分析人员。
- 用户和分析人员拥有数据,如
Table 1和Table 2所示 - 对于
Algorithm 1的每个步骤都由相应的角色执行,如Figure 1所示 - 对于每个映射函数 \(f_i\),由以下要求构建:
- 原始数据只能使用中间表示和映射函数\(f_i\)或其近似来近似。
- 映射函数 \(f_i\) 只能使用 \(f_i\)的输入和输出数据来近似。
- 分析人员不会与用户串通以获得其他用户的原始数据。
在这样的操作策略中,每个用户不拥有其他用户的中间表示,分析人员不具有又是锚点数据 \(X^{anc}\)。因此,原始数据集 \(X_i\)不能被其他人获取。证明原始数据 \(X_i\) 的隐私权在我们的定义中得到保留。


数值实验
在我们的目标情况下,应该注意集中分析是理想的,因为没有共享原始数据集 \(X_i\)。我们提出的数据聚合分析必须实现比单个分析更高的识别性能,但要比集中分析的识别性能低,但与集中分析结果近似。
这里使用核岭回归(Kernel Ridge Regression)来对单独和集中分析,以及第八步中的操作。在算法中,每个中间表示都由 \(X_i\) 使用核LPP (K-LPP)来构造。注意到 K-LPP是一种无监督的将为方法。构建的映射 \(f_i\)取决于 \(i\)因为它需要基于数据集 \(X_i\)。锚点数据采用一个随机矩阵构建。
在训练阶段,我们使用真实标签 \(L\)作为一个二元矩阵,若训练数据\(x_j\)为\(i\)类,则其每一项 \((i, j)\) 即为 1。所有的实验都在 MATLAB上完成。
人造数据
这个实验使用了一个三类的十维人造数据。Figure 2(a)显示了真实标签的前两维。Figure 2(b-d) 显示了每个用户数据集中有40个训练数据点的前两维的映射,并带有相应的标签:∘, •, and +。我们使用一个 \(201 \times 201\) 数据点作为测试集,前两维从 \([-1, 1] \times [-1, 1]\) 方格中均匀选取。训练和测试数据的其余八个维度是由 Mersenne Twister 随机生成器,从 \([-0.1, 0.1]\) 之间抽取的随机值。所有方法都采用高斯核。
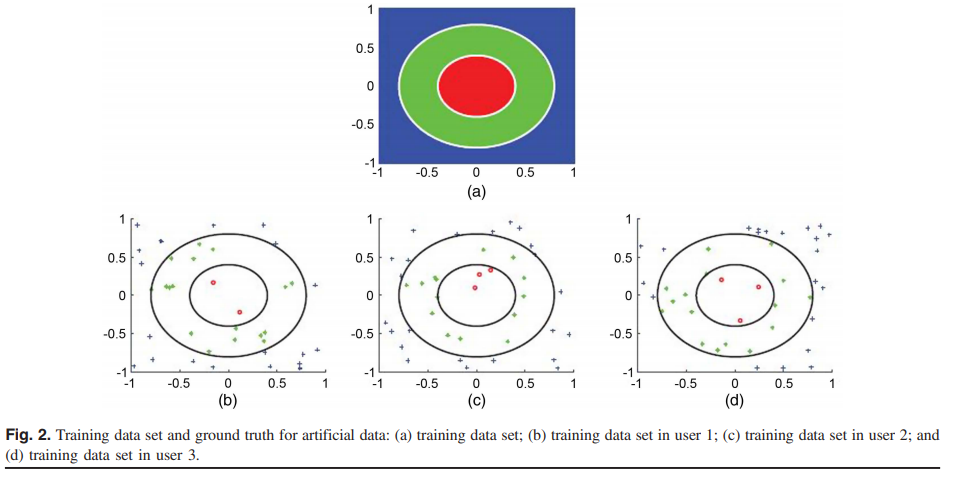
集中分析的准确性 (AAC) ,三个用户分别评估的平均AAC,以及提出的数据聚合分析的为 92.3,79.8和 91.3。Figure 3 展现出了识别结果。
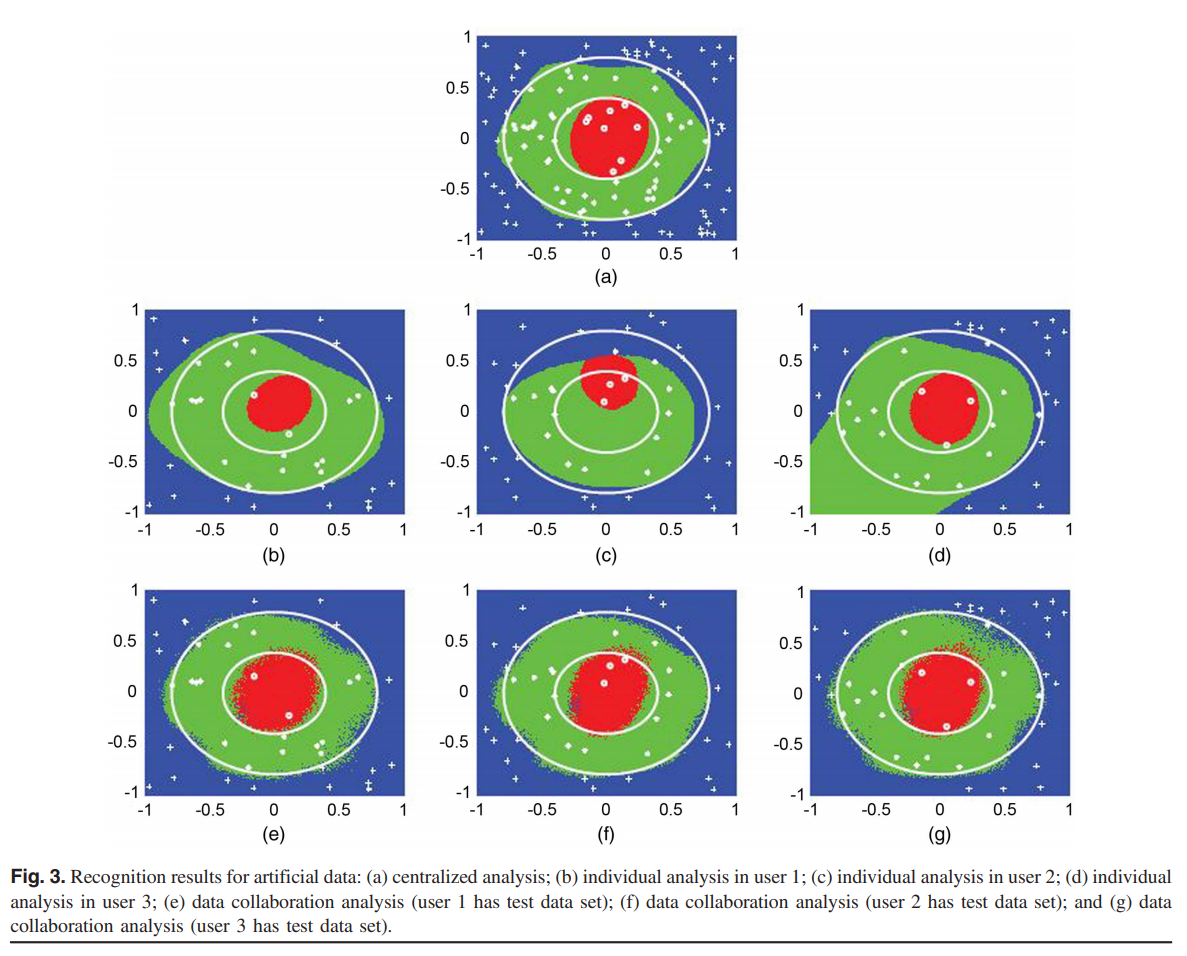
我们观察到,由于数据样本不足,个人分析的识别结果明显差于集中分析的识别结果。 相反,所提出的数据聚合分析所获得的结果可与直接集中分析的结果相媲美。
MNIST
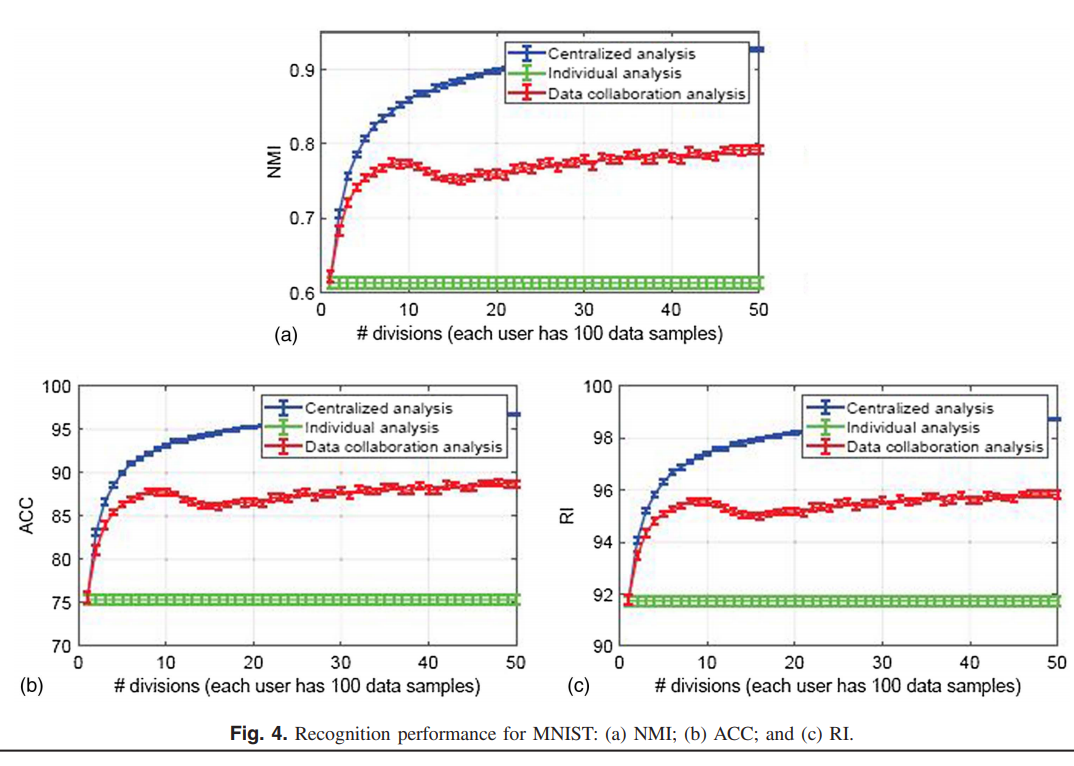
手写数据集分为10类,且维度为 784 维。我们为每个用户设置了100个数据样本,并针对1000个测试数据样本评估了识别性能,归一化互信息(NMI),准确性(ACC),兰德指数(RI),使用户数量从1增加到50。 所有方法都采用高斯核。
Figure 4 显示了每种方法20次试验的识别性能的平均值和标准差。可以看出,所提出的数据协作分析的识别性能随着用户数量的增加而增加,并且比单个分析获得了更高的识别性能。
基因数据
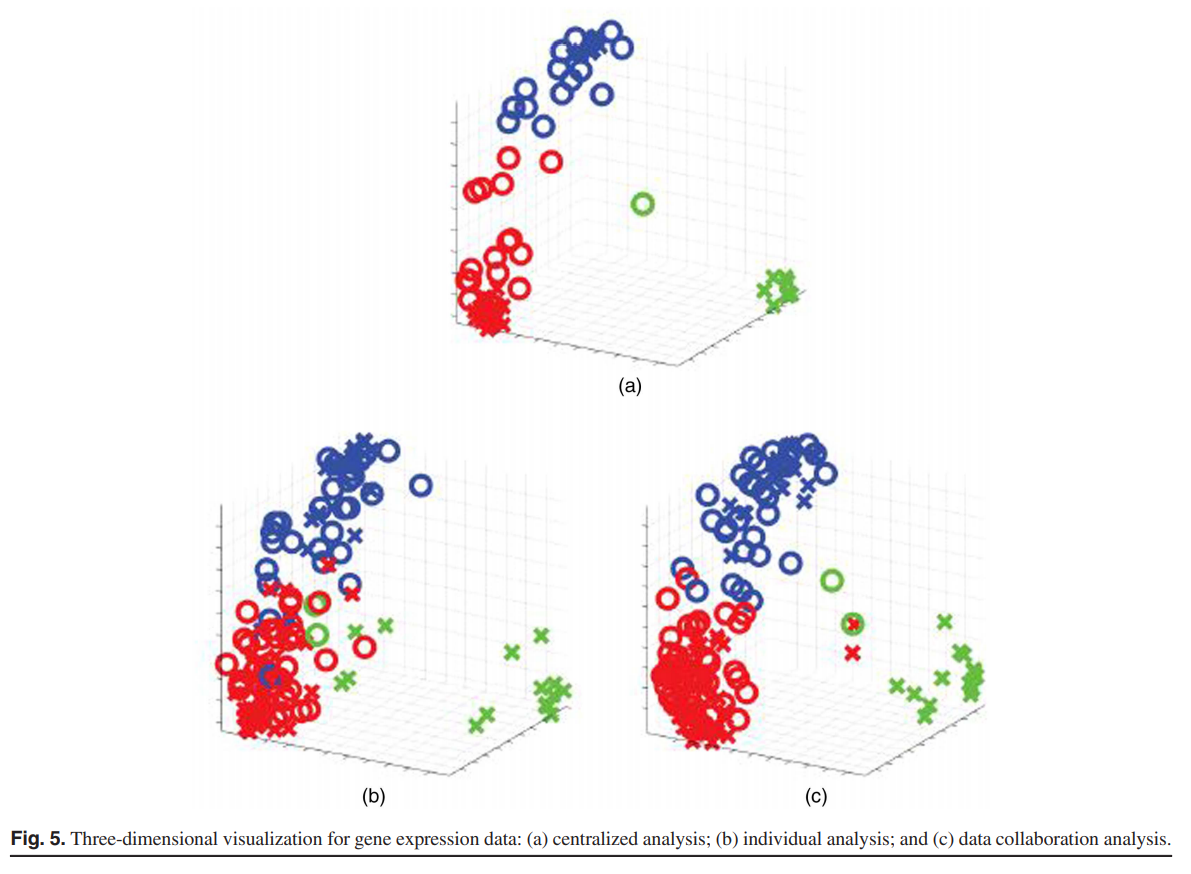
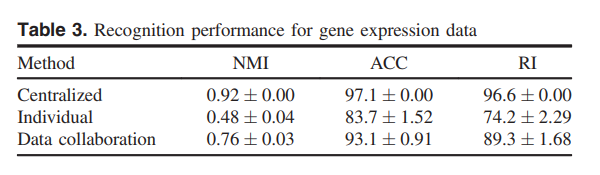
我们还是用了三分类癌症数据。该数据集具有 38个训练数据和34个测试数据样本,其中数据具有 7129个特征。在这里,我们考虑了两个用户的情况,并为每个用户分配了19个数据样本。接下来,我们评估了20个试验的识别性能。 所有方法均使用线性核。
Figure 5 将训练数据和测试数据分别用 + 和 ∘ 表示出来。Table 3 总结了了识别性能(平均值和标准差)。在三维可视化中,提出的数据聚合分析和集中式分析构建的低维空间中,三个类别被很好地分隔开。我们观察到,对于真实问题,我们提出的数据聚合分析比单个分析具有更高的识别性能。
数值结果说明
数值实验的结果表明,该数据聚合分析对人工和现实世界的数据集的识别性能要高于单数据集分析。 应该注意的是,因为集中分析是理想的,所以所提出的数据聚合分析的识别性能不需要比集中分析的识别性能高。
结论
本文提出了一种基于集中分布式单数据集中间表示的数据聚合分析框架,原始数据和映射函数仍然保持分布式。本文还提出了框架内的使用算法和关于数据隐私的实践操作策略。与现有方法不同,该框架不适用隐私保护计算,也不需要集中映射函数。数值实验表明,与单独分析相比,该方法对(单一的)人工和真实数据集具有更高的识别性能。