简介
子空间聚类旨在将一系列未标记的样本从一组对应于不同聚类的多个子空间集合中分割成几组。最近,基于自我表征的模型在子空间聚类中取得了卓越的性能。它假设一个样本可以由一组样本的线性组合来表示:
\[\underset{Z}{\min} L(X, Z) + R(Z),\ s.t. X=XZ,\]其中,\(X \in \mathbb{R}^{d\times n}\) 且 \(Z \in \mathbb{R}^{n\times n}\) 分别代表训练数据和自我表征向量、\(L(X, Z)\)代表了重建误差,\(R(Z)\)为正则项。
基于自我表征的子空间聚类模型的主要区别在于损失函数和正则项的选择。对于正则项来说,在特定的子控件假设中,l0-norm, l1-norm, square of Frobenius
norm, elastic net, trace Lasso 和 k-block diagonal regularizer 都有被使用过。由于手工特征不能很好捕捉大量变种的信息,深度子控件聚类模型被用于联合学习层级表示和聚类结构。
如 Figure 1 所示,通过收集包括文字、图像、音频、和视频的数据来表征一个样本。对于单模态数据,例如图片或视频序列,可以提取各种特征以捕获比例,遮挡,照明,旋转变化,以实现可靠的识别效果。总的来说,多视角学习涵盖了多模态和多特征学习。多模态和多特征信息可以被合成来增加子控件聚类的性能。
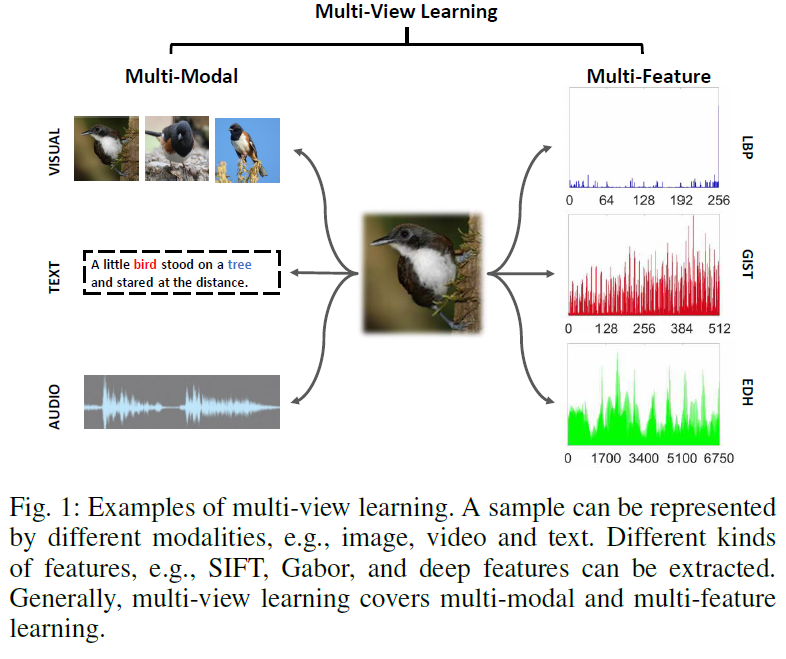
多视角子空间聚类(MVSC)旨在利用以不同方式手机的数据或以不同类型的特征表示的数据来发现底层的聚类结构。大多数 MVSC方法设计多视图正则项来表征集中类型的手工特征之间的视图间关系,来实现多视图聚类。
然而有两点不尽人意:
- 当前的方法采取一种二级策略:先提取特征再学习近似矩阵。特征提取过程与子空间聚类聚类任务并不相关。多视角关系只能在近似矩阵学习过程中,忽视了特征学习中视图间关系。
- 没有考虑对于层级表示学习的端到端学习。
本文提出了一种以学习多视角自我表征矩阵的端到端多视角的深度子空间聚类网络(MvDSCN)。 MvDSCN由差异网络(Dnet)和共性网络(Unet)组成。 Dnet学习特定视图的自我表征矩阵(\(Z_1, Z_2, \cdots, Z_v\)),Unet 学习一个通用的自我表征矩阵 \(Z\)。使用手工特征或原始数据作为输入,为每个视图学习深度卷积自动编码器。同时将多视图重建和自我表征损失最小化。 为了利用互补的多视图信息,使用了Hilbert Schmidt Independence Criterion (HSIC)来定义了一个多样化正则项。另外,还使用了一个通用正则器来使特定视角的 \(Z_i\)接近通用 \(Z\)。通过多样和通用正则化,多视图关系很好地嵌入了特征学习和自我表征阶段。多特征和多模态聚类的实验证明了所提出的模型优于最新的子控件聚类方法的优越性。
相关工作
多视角聚类
子空间聚类旨在从包含多个子空间的数据中发现固有的聚类结构。基于自我表征的子空间聚类方法基本上都是基于学习到一个好的相似矩阵并进行频谱聚类这一假设,即可以通过其他样本的线性组合来重建样本。深度子空间聚类网络通过全连接层将自我表征嵌入到深度卷积自编码器中。深度对抗子空间聚类使用类似GAN的模型来评估聚类性能,加入了自我表征损失。
多视图聚类通过对视图间关系建模或学习潜在表示来探索补充信息,从而提高了聚类的性能。大多数现有的多视图聚类方法都可以视为单视图模型的扩展。多视图关系通常可以分为普遍性和多样性。普遍性强调所有视角的相似之处,而多样性则集中于视角之间的互补性,从而导致了不同视图的特定表示。现有的多视图子空间聚类方法将多视图特征提取和相似性学习视为两个单独的阶段。 另外,由于特定于视图的特性,强制所有视图的自表示矩阵相同是不合理的。
自我表征
自我表征反映了样本之间的内在联系,并已广泛用于图像处理,聚类,特征选择和深度学习。在图像处理中,尤其是图像去噪中,非局部均值已被广泛使用,它使用图像中的相关像素或块来重建像素或图像块,这激发了许多成功的低层图像处理模型。除了像素级别的自我表征外,还可以通过bases的线性组合很好地重构样本。自我表征已经成功运用于聚类中,因为它可以通过嵌入稀疏、密集或低秩先验值来准确捕获样本关系。为了减轻高维诅咒,特征选择旨在通过评估特性的重要性来选择特征子集。特征级的自我表征假设一个特征可以由所有特征重建,并且自我表征系数可以用于特征评估。
自编码器
自编码器通过将数据映射到低维空间来提取数据特征。深度自动编码器已广泛用于降维和图像去噪。由于卷积层比全连接层具有更少的参数和更强的学习能力,因此可以以端对端的方式训练的卷积自动编码器(CAE)被设计用于从未标记的数据中进行特征学习。
多视角深度子空间聚类
网络架构
令 \(X_1, \cdots, X_i, \cdots, X_v\) 表示输入的多视角,其中 \(X_i \in \mathbb{R}^{n\times d_i}\),\(v, n\) 和 \(d_i\) 分别代表视角的数量,样本,以及第\(i\)个视角的特征。\(X_i\) 可以使手工特征或生数据,例如图片或深度图像数据。多视角深度子空间聚类的架构如Figure2 所示。
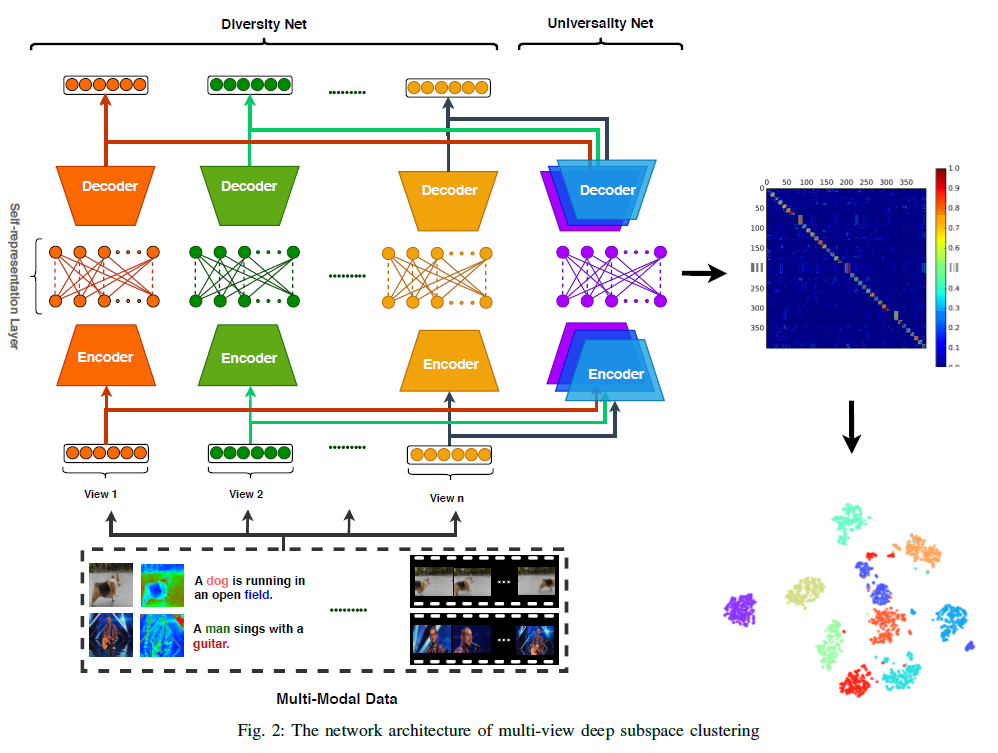
本文提出的网络由两部分组成,即差异网络 (Dnet) —— 学习单独视角的表示 和 共性网络 (Unet) —— 共享视图一致的自我表征矩阵。
Dnet 将使用特定视角的编码器将输入的 \(X_i\)嵌入到隐含表示 \(F_i^s\) 中。然后,通过无偏置和非线性激活的全连接层进行自我表征,即 \(F_i^s = F_i^s Z_i\)。 Unet 对所有视角共享了一个公共自我表征矩阵 \(Z\),与其他所有隐含表示相关 \(F_1^c, F_2^c, \cdots, F_v^c\)。在自我表征层之后,样本将由特定视角的解码器复原。
对于这两者,我们都使用参数较少且学习能力较强的卷积自动编码器,而不使用全连接层。我们分别使用具有 [64、32、16]通道的三层编码器和具有[16、32、64]通道的三层解码器。 我们采用 \(3\times 3\)卷积核核和ReLU进行非线性激活,没有使用池化层。 然后,隐特征通过转置卷积层返回到与输入相同大小的空间。
损失函数
损失函数包括两部分,即自编码器的重建loss和自我表征loss。
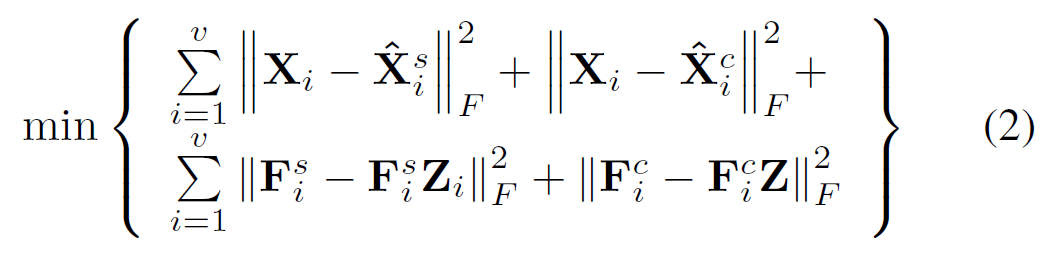
为了将多视角关系嵌入到特征学习和自我表征当中,使用了两种类型的正则项。为了从多视角中(例如 RGB信息和深度信息)中利用补充信息,基于Hilber Schmidt独立标准 (HSIC)定义了分级正则化。HSIC 测量非线性和高阶相关性,并已成功用于多视图子空间聚类中。
我们假设有两个变量 \(A = [a_1, \cdots, a_i, \cdots, a_N]\) 和 \(B = [b_1, \cdots, b_i, \cdots, b_N\),我们可以定义一个映射 \(\phi(a)\) 从 \(a \in \mathfrak{A}\)到核空间 \(\mathfrak{F}\),其中两个向量的内积可以定义为 \(k( a_{1} ,a_{2}) =\langle \phi ( a_{1}) ,\phi ( a_{2}) \rangle \)。 \(\varphi (b)\) 定义为将 \(b \in \mathfrak{B}\)映射到核空间 \(\mathfrak{R}\)。同样的,在核空间 \(\mathfrak{R}\) 中两个向量的内积为 \(g( b_{1} ,b_{2}) =\langle \varphi ( b_{1}) ,\varphi ( b_{2}) \rangle \)。HSIC的经验版本可以归纳为:
定义1:考虑一系列 \(N\) 个从\(p_{ab}\)中抽取的独立观察点,\(Z:={(a_1, b_1), \cdots, (a_N, b_N)} \subseteq \mathfrak{A}\times \mathfrak{B}\)。HSIC可以写为:
\(\mathrm{HSIC}(\mathfrak{Z} ,\ \mathfrak{F} ,\mathfrak{B}) \ =\ ( N-1)^{-2} tr(\mathbf{G}{1}\mathbf{HG}{2}\mathbf{H})\)
其中,\(tr(\cdot)\)是方阵的迹,\(\mathbf{G}{1}\)和 \(\mathbf{G}{2}\) 是Gram矩阵,且 \(g_{1,ij} =g_{1}( a_{i} ,a_{j}) ,g_{2,ij} =g_{2}( b_{i} ,b_{j})\)。\(h\index{ij}=𝛿\index{ij}-1/N\) 使在特征空间中均值为零的Gram矩阵居中。
基于HSIC,差异正则项定义为:
\(R_d(Z_1, Z_2, \cdots, Z_v) = \Sum_{ij} \mathrm{HSIC}(Z_i, Z_j)\)
该正则项可以从多视角有效地利用补充信息。由于所有的视图共享相同的决策空间,因此反映样本关系的特定于视图的自我表征矩阵应与Unet中的共有自我表征矩阵对齐。我们定义了一个集中化正则项如下所示:
\(R_c(Z, Z_1, Z_2, \cdots, Z_v) = \Sum^v_{i=1} | Z-Z_i|_F^2\)
考虑了多视图的关系,目标函数变为:
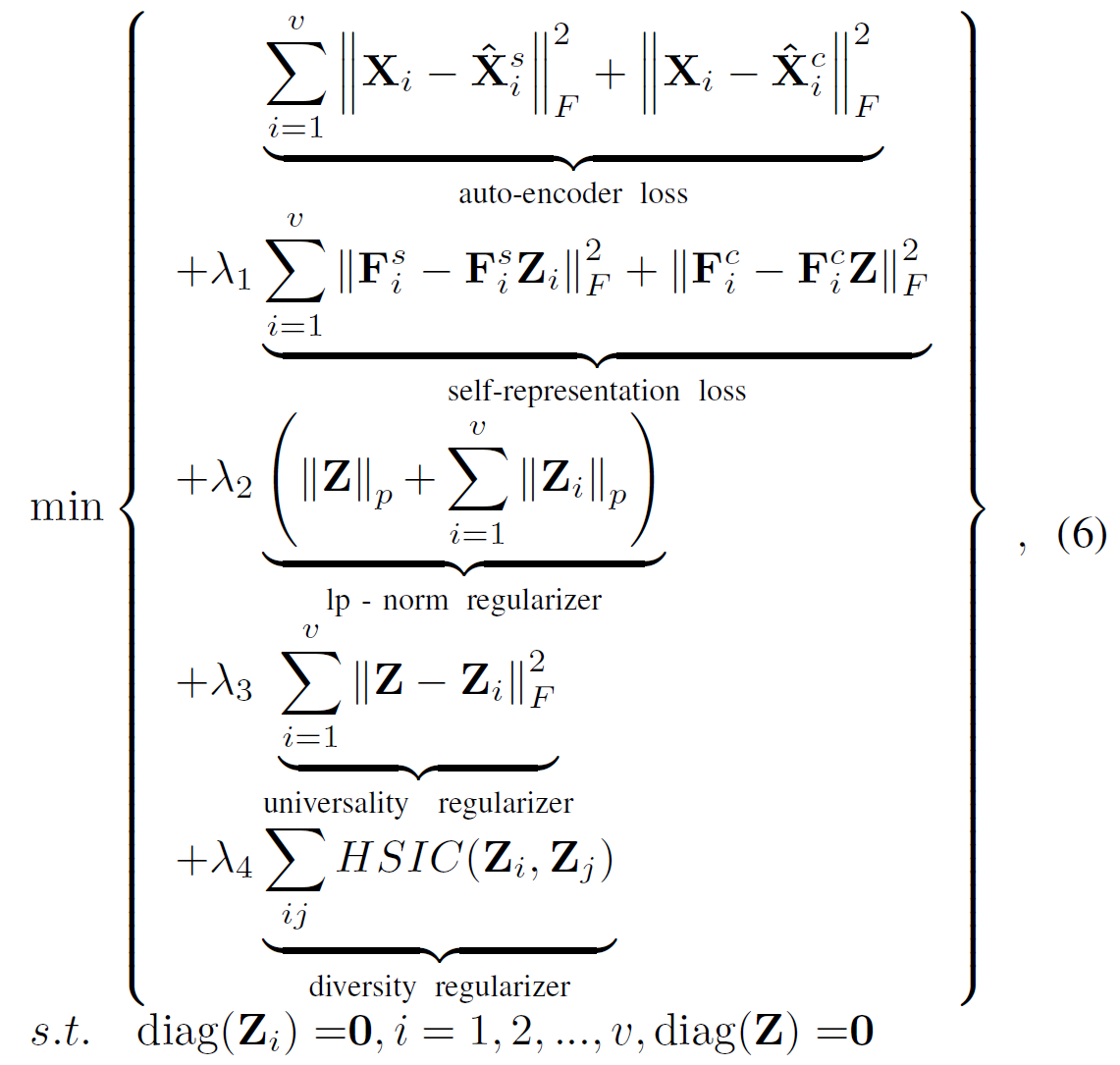
其中,\(\lambda_1, \lambda_2, \lambda_3 \) 和 \(\lambda_4\) 为正常数,\(|Z|_p\)是 \(Z\)的\(l_p\)范数。这里我们也考虑其他的正则项,例如核心归一和块对角正则项。

MvDSCN获知的亲和度矩阵具有更好的块对角线属性和更少的噪声。
优化
当我们使用Frobenius范数正则化的平方时,\(Z_i\) 的梯度为:
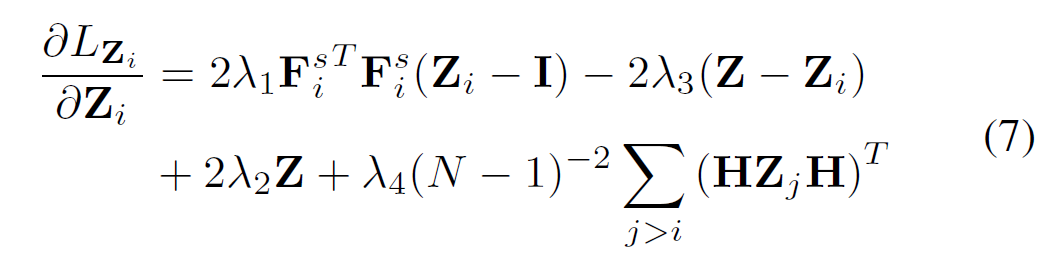
\(Z\) 的梯度为:
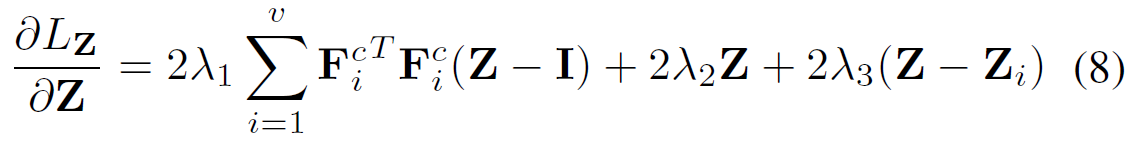
我们首先在所有多视图数据上对不加入自我表征层的深度自动编码器进行预训练,因为网络很难直接从头开始训练,并且在最小化损失函数的同时避免了琐碎的全零解。 然后,我们使用预训练的参数来初始化Dnet和Unet的卷积编码器/解码器层。 在微调阶段,我们使用所有数据构建一个大批处理,以最小化损失函数。 该模型由Adam训练,初始学习率为0.001。
对于自我表征损失和lp-norm正则项的正则化超参数,我们通常设置\(\lambda_1 = 1.0 \times 10^{\frac{k}{10}-3}\),其中 \(k\) 是子空间的数量,\(\lambda_2 = 1.0, \lambda_3 = 0.1, \lambda_4=0.1\)。
| 我们的网络将联合更新Dnet和Unet。 网络收敛后,我们可以对所有视图使用公共自表达层的参数,以构建用于谱聚类的亲和矩阵\( | Z | + | Z | ^T\)。 |
Alg 1中总结了解决MvDSCN的算法。

讨论
多视图子空间聚类的最新工作集中在通过字典学习或矩阵分解来学习跨视图的潜在表示。 为\(X\)学习一个潜在表示\(C\),然后在\(C\)上进行自我表示。
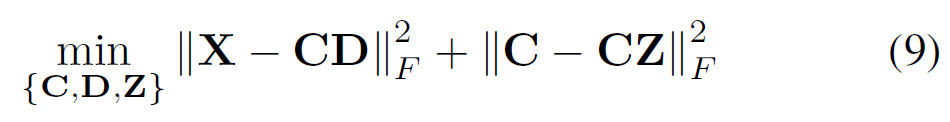
与基于潜在表示的方法相比,MvDSCN还通过自动编码器\(\phi\)来学习隐藏表示\(F\)。自编码器可以视为将输入投射到潜在空间的映射功能。
MvDSCN具有以下两个优点:1)与现有的浅层模型相比,通过使用深度卷积自动编码器,无论输入\(X\)是手工特征还是原始数据,隐藏表示\(F\)的信息量都更大。 2)MvDSCN以端到端的方式将学习和自我表征结合在一起。 因此,多视图关系可以指导亲和矩阵学习和特征学习。 因此,MvDSCN可以学习良好的亲和度矩阵,从而提高多视图子空间聚类的性能。