Original Paper: A Survey of Clustering with Deep Learning from the Perspective of Network Architecture
Header Photo: From Unsplash
Preliminary
Loss Functions Related to Clustering
Generally, there are two kinds of clustering loss.
- Principal Clustering Loss: After the training of network guided by the clustering loss, the clusters can be obtained directly. It includes k-means loss, cluster assignment hardening loss, agglomerative clustering loss, nonparametric maximum margin clustering.
- Auxiliary Clustering Loss: These kinds of loss guiding the network to learn a more feasible representation for clustering, but cannot output clusters straightforwardly, such as locality-preserving loss, group sparsity loss, sparse subspace clustering loss.
Performance Evaluation Metrics for Deep Clustering
The first metric is unsupervised clustering accuracy (ACC):
\[ACC = \underset{m}{\mathrm{max}}\frac{\sum _{i=1}^{n} 1\{y_{i} =m( c_{i})\}}{n}\]where \(y_i\) is the ground-truth label, \(c_i\) is the cluster assignment generated by the algorithm, and \(m\) is a mapping function which ranges over all possible one-to-one mappings between assignments and labels. The optimal mapping function can be efficiently computed by Hungarian algorithm.
The second one is Normalized Mutual Information (NMI):
\[NMI(Y, C) = \frac{I(Y, C)}{\frac{1}{2}[H(Y) + H(C)]}\]where \(Y\) denotes the ground-truth labels, \(C\) denotes the clusters labels, \(I\) is the mutual information metric and \(H\) is entropy.
Taxonomy of Deep Clustering
The loss function of deep clustering methods are typically composed of two parts: network loss \(L_n\) and clustering loss \(L_c\), thus the loss function can be formulated as follows:
\[L = \lambda L_n + (1-\lambda)L_c\]where \(\lambda \in [0, 1]\) is a hyper-parameter to balance \(L_n\) and \(L_c\). The network loss \(L_n\) is used to learn feasible features and avoid trivial solution, and the clustering loss \(L_c\) encourages the feature points to form groups or become more discriminative.
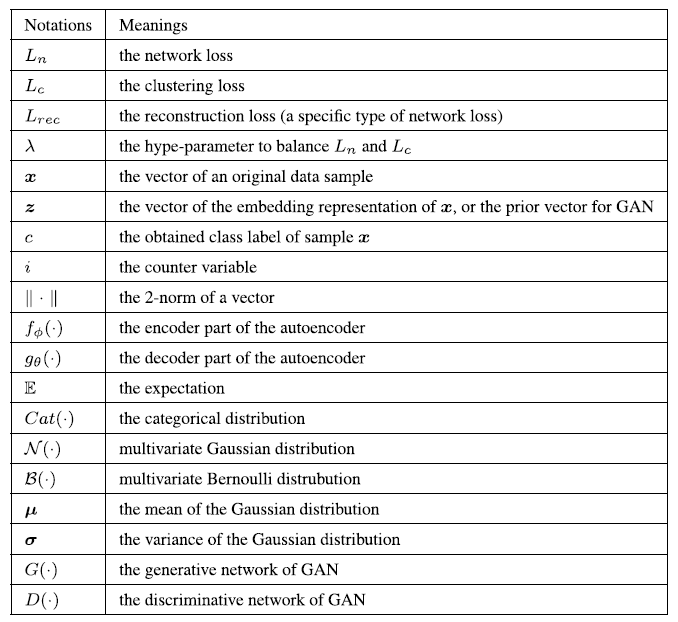
AE-Based Deep Clustering
Autoencoder aims at minimizing the reconstruction loss. An autoencoder may be viewed as consisting of two parts: an encoder function \(h=f_\phi (x)\) which maps original data \(x\) into a latent representation \(h\), and a decoder that produces a reconstruction \(r=g_\theta(h)\). The reconstructed representation \(r\) is required to be as similar to \(x\) as possible.
When the distance measure of the two variables is MSE, given a set of data samples \({x_i}^n_{i=1}\), its optimizing objective is formulated as follows:
\[\underset{\phi, \theta}{\mathrm{min}} L_{rec} = \min \frac{1}{n} \sum^n_{i=1} \| x_i - g_\theta(f_\phi(x_i)) \|^2.\]where \(\phi\) and \(\theta\) denote the parameters of encoder and decoder respectively.
The performance of autoencoder can be improved from the following perspectives:
- Architecture: For the sake of handling data with spatial invariance, such as image data, convolutional and pooling layers can be used to construct a convolutional autoencoder (CAE).
- Robustness: To avoid overfitting and to improve robustness, it is natural to add noise to the input. Denoising autoencoder attempts to reconstruct \(x\) from \(\tilde{x}), which is a corrupted version of \(x\) through some form of noise.
- Restriction on latent features: Under-complete autoencoder constrains the dimension of latent coder \(z\) lower than that of input \(x\), enforcing the encoder to extract the most salient features from original space.
- Reconstruction loss: Commonly the reconstruction loss of an autoencoder consists of only the discrepancy between input and output layer, but the reconstruction losses of all layers can also be optimized jointly.
The optimizing objective of AE-based deep clustering is thus formulated as follows:
\[L = \lambda L_{rec} + (1 - \lambda) L_c\]The reconstruction loss enforce the network to learn a feasible representation and avoid trivial solutions.
Representative methods:
- Deep Clustering Network: DCN combines autoencoder with the k-means algorithm. In the first step, it pre-trains an autoencoder. Then, it jointly optimizes the reconstruction loss and k-means loss. Since k-means uses discrete cluster assignments, the method requires an alternative optimization algorithm. The objective of DCN is simple compared with other methods and the computational complexity is relatively low.
- Deep Embedding Network: DEN proposes a deep embedding network to extract effective representation for clustering. It first utilizes a deep autoencoder to learn reduced represetnation from the raw data. Secondly, in order to preserve the local structure property of the original data, a locality preserving constraint is applied. Futhermore, it also incorporates a group sparsity constraint to diagonalize the affinity of representations. Together with the reconstructuion loss, the three losses are jointly optimized to fine-tune the network for a clustering-oriented representation. The locality-preserving and group spasity constraints serve as the auxiliary clustering loss, thus, as the last step, k-means is required to cluster the learned representations.
- Deep Subspace Clustering Networks: DSC-Nets introduces a novel autoencoder architecture to learn an explicit non-linear mapping that is friendly to subspace clustering. The key contribution is introducing a novel self-expressive layer, which is a fully connected layer without bias and non-linear activation and inserted to the junction between the encoder and the decoder. This layer aims at encoding the self-expressiveness property of data drawn from a union of subspaces. Mathematically, its optimizing objective is a subspace clustering loss combined with a reconstruction loss.
- Deep Multi-Manifold Clustering: DMC is deep learning based framework for multi-manifold clustering. It optimizes a joint loss function comprised of two parts: the locality preserving objective and the clustering-oriented objective. The first part makes the learned representations meaningful and embedded into their intrinsic manifold. It includes the autoencoder reconstruction loss and locality preserving loss. The second part penalizes representations based on their proximity to each cluster centroids, making the representation cluster-friendly and discriminative.
- Deep Embedded Regularized Clustering (DEPICT): It consists of a softmax layer stacked on top of a multi-layer convolutional autoencoder. It minimizes a realtive entropy loss function with a regularization term for clustering. The regularization term encourages balanced cluster assignments and avoids allocating clusters to outlier samples. Futhermore, the reconstruction loss of autoencoder is also employed to prevent corrupted feature representation.